1. (1)兩角和
它們的夾邊
分別相等的兩個(gè)三角形全等(可以簡(jiǎn)寫成
角邊角
或
ASA
).
(2)兩角
分別相等
且其中
一組等角的對(duì)邊相等
的兩個(gè)三角形全等(可以簡(jiǎn)寫成
角角邊
或
AAS
).
答案:1.(1)它們的夾邊 角邊角 ASA
(2)分別相等 一組等角的對(duì)邊相等 角角邊 AAS
2. 符號(hào)語言:
(1)如圖,在$\triangle ABC和\triangle DEF$中,
$\left\{\begin{array}{l} ∠A=
∠D
,\\
AB
=
DE
,\\
∠B
= ∠E,\end{array} \right.$
$\therefore \triangle ABC\cong \triangle DEF$(
ASA
).
(2)如圖,在$\triangle ABC和\triangle DEF$中,
$\left\{\begin{array}{l} ∠A=
∠D
,\\
∠B
= ∠E,\\
BC
=
EF
,\end{array} \right.$
$\therefore \triangle ABC\cong \triangle DEF$(
AAS
).
答案:2.(1)∠D AB DE ∠B ASA
(2)∠D ∠B BC EF(或 AC DF) AAS
1. 如圖,已知O是AB的中點(diǎn),$∠A= ∠B$,求證:$\triangle AOC\cong \triangle BOD.$
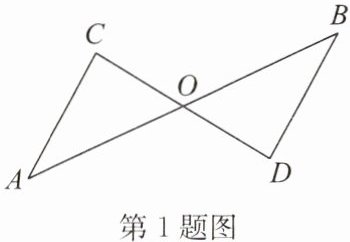
答案:證明:∵O是AB的中點(diǎn),∴AO=BO.
在△AOC和△BOD中,∠A=∠B,
AO=BO,
∠AOC=∠BOD,
∴△AOC≌△BOD(ASA).
2. 如圖,$AB⊥BC,AD⊥DC,∠1= ∠2$. 求證:$CB= CD.$

答案:證明:∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°.
在△ABC和△ADC中,∠1=∠2,
∠B=∠D,
AC=AC,
∴△ABC≌△ADC(AAS),∴CB=CD.
3. 如圖,兩車從路段AB的兩端同時(shí)出發(fā),沿平行路線以相同的速度行駛,相同時(shí)間后分別到達(dá)C,D兩地.C,D兩地到路段AB的距離相等嗎? 為什么?

答案:解:C,D兩地到路段AB的距離相等.理由如下:
由題意可知AC=BD.
∵CE⊥AB,DF⊥AB,∴∠AEC=∠BFD=90°.
∵AC//BD,∴∠A=∠B.
在△AEC和△BFD中,∠AEC=∠BFD,
∠A=∠B,
AC=BD,
∴△AEC≌△BFD(AAS),∴CE=DF.
即C,D兩地到路段AB的距離相等.