1. 三邊
分別相等
的兩個(gè)三角形全等(可以簡(jiǎn)寫成
邊邊邊
或
SSS
).
答案:分別相等 邊邊邊 SSS
如圖,在$\triangle ABC和\triangle DEF$中,
DE
=
AC
,
DF
=
BC
,∴$\triangle ABC\cong \triangle DEF$(
SSS
).
答案:DE AC DF BC SSS
解析:
在$\triangle ABC$和$\triangle DEF$中�,
$\left\{\begin{array}{l} AB=DE\\ AC=DF\\ BC=EF\end{array}\right.$
$\therefore \triangle ABC\cong \triangle DEF(SSS)$
1. 如圖是一個(gè)平分角的儀器,其中$AB= AD$,$BC= DC$.將點(diǎn)$A$放在一個(gè)角的頂點(diǎn),$AB和AD$沿著這個(gè)角的兩邊放下,利用全等三角形的性質(zhì)就能說明射線$AC$是這個(gè)角的平分線,這里判定$\triangle ABC和\triangle ADC$是全等三角形的依據(jù)是
SSS
.
答案:SSS
2. 如圖,$AB= AD$,$BC= CD$.求證:$\angle B= \angle D$.
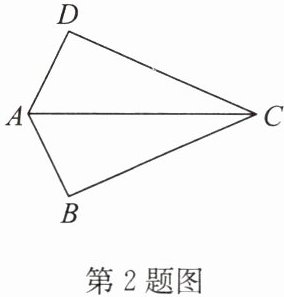
答案:證明:在△ABC和△ADC中,
{AB=AD��,
BC=DC��,
AC=AC��,
∴△ABC≌△ADC(SSS)����,∴∠B=∠D.
3. (2024·江寧區(qū)模擬)如圖是小明制作的風(fēng)箏,他根據(jù)$DE= DF$,$EH= FH$,不用測(cè)量,就知道$\angle DEH= \angle DFH$.小明是通過全等三角形的知識(shí)得到的結(jié)論,請(qǐng)幫他說明理由.

答案:解:在△DHE和△DHF中,
{DH=DH�����,
DE=DF��,
EH=FH���,
∴△DHE≌△DHF(SSS)��,∴∠DEH=∠DFH.