1. 兩邊和它們的夾角
分別相等
的兩個(gè)三角形全等(可以簡(jiǎn)寫成
邊角邊
或
SAS
).
答案:分別相等 邊角邊 SAS
如圖,在$\triangle ABC和\triangle DEF$中,
$\left\{\begin{array}{l} AB=
DE
, \\
∠B
=
∠E
, \\
BC
= EF, \end{array} \right.$
$\therefore \triangle ABC\cong \triangle DEF(
SAS
)$
答案:DE ∠B ∠E BC SAS
解析:
在$\triangle ABC$和$\triangle DEF$中,
$\left\{\begin{array}{l} AB=DE, \\ ∠B=∠E, \\ BC=EF, \end{array} \right.$
$\therefore \triangle ABC\cong \triangle DEF(SAS)$
1. 如圖,點(diǎn)$B,F,C,E$在同一條直線上,$AB= DE,BF= CE,AB// DE$,求證:$AC= DF$.
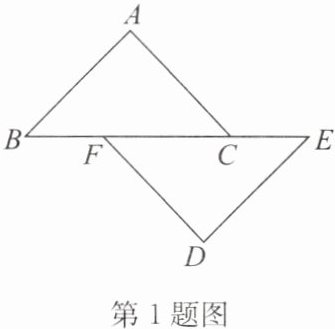
答案:證明:∵AB//DE,∴∠B=∠E.
∵BF=CE,∴BF+FC=CE+FC,即 BC=EF.
又 AB=DE,∴△ABC≌△DEF(SAS).∴AC=DF.
2. 如圖,$AB= AD,AC= AE,∠BAE= ∠DAC$. 求證:$∠C= ∠E$.

答案:證明:∵∠BAE=∠DAC,
∴∠BAE+∠CAE=∠DAC+∠CAE,
即∠CAB=∠EAD,又 AB=AD,AC=AE,
∴△ABC≌△ADE(SAS),∴∠C=∠E.
3. (2024春·成都期末)某數(shù)學(xué)興趣小組的同學(xué)測(cè)量一個(gè)小口圓形容器內(nèi)徑時(shí)遇到了困難,小組同學(xué)們借用學(xué)過(guò)的三角形全等的知識(shí)合作制作了特制工具測(cè)量器. 如圖所示,將等長(zhǎng)的鋼條$AD和BC的中點(diǎn)O$焊接在一起,制作了一把“X”形卡鉗. 根據(jù)“X”形卡鉗的制作原理能判斷$\triangle ABO\cong \triangle DCO$,從而測(cè)量出$AB$的長(zhǎng),就等于內(nèi)徑$CD$的長(zhǎng). 請(qǐng)寫出$\triangle ABO\cong \triangle DCO$的理由.

答案:解:在△AOB 和△DOC 中,
OA=OD,
∠AOB=∠DOC,
BO=CO,
∴△AOB≌△DOC(SAS).