在直角三角形中,如果一個銳角等于$30^{\circ }$,那么它所對的直角邊等于
斜邊的一半
.
答案:斜邊的一半
1. 如圖,小明沿傾斜角$∠ABC= 30^{\circ }$的山坡從山腳 B 點步行到山頂 A,共走了 500 m,則山的高度 AC 是
250 m
.
答案:250 m
解析:
在Rt△ABC中�,∠ACB=90°���,∠ABC=30°���,AB=500m。
因為在直角三角形中��,30°角所對的直角邊等于斜邊的一半����,
所以AC=AB×$\frac{1}{2}$=500×$\frac{1}{2}$=250m����。
250 m
2. 如圖,在$△ABC$中,$∠A= 30^{\circ },AB= BC$,點 D,E 分別在邊 AB,AC 上,若沿直線 DE 折疊,點 A 恰好與點 B 重合,且$CE= 6$,則$∠EBC= $
90
$^{\circ },AC= $
9
.
答案:90 9
解析:
解:在△ABC中��,AB=BC���,∠A=30°��,
∴∠A=∠C=30°�����,∠ABC=180°-30°-30°=120°���。
由折疊知,DE垂直平分AB���,AE=BE�����,
∴∠A=∠ABE=30°����,
∴∠EBC=∠ABC-∠ABE=120°-30°=90°。
在Rt△BEC中�����,∠C=30°����,CE=6,
∴BE=1/2CE=3��,
∴AE=BE=3���,
∴AC=AE+CE=3+6=9。
∠EBC=90°�����,AC=9��。
3. 如圖,在等邊$△ABC$中,M 是 BC 的中點,$MN⊥AB$,垂足為 N,連接 AM,求證:$AM= 2MN.$
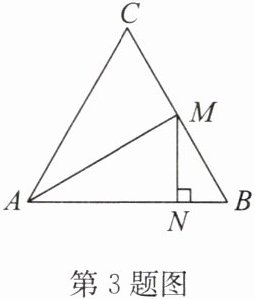
答案:證明:∵△ABC 為等邊三角形��,
∴AB=AC,∠BAC=60°.
∵M 為 BC 的中點�����,
∴AM⊥BC,∠BAM=$\frac{1}{2}$∠BAC=30°.
∵MN⊥AB,∴AM=2MN.
4. (2024 春·錦江區(qū)期末)如圖,在等邊$△ABC$中,BD 平分$∠ABC$,點 E 是 BC 延長線上一點,且$CE= CD$,連接 DE,求$∠BDE$的度數(shù).

答案:解:∵△ABC 為等邊三角形,
∴∠ABC=∠ACB=60°�����,
∵BD 平分∠ABC�,
∴∠ABD=∠CBD=30°,BD⊥AC,
即∠BDC=90°.
∵CE=CD����,
∴∠CDE=∠E,
∵∠ACB=∠CDE+∠E�����,
∴2∠CDE=60°��,
∴∠CDE=30°����,
∴∠BDE=∠BDC+∠CDE=90°+30°=120°.
5. 如圖,在$△ABC$中,$∠C= 90^{\circ },∠B= 30^{\circ }$,DE 是 AB 的垂直平分線,垂足為 E,DE 交 BC 于點 D,連接 AD.
(1)求證:$DC= DE;$
(2)若$CD= 3$,求 BD 的長.

答案:(1)證明:∵DE 是 AB 的垂直平分線,∴DA=DB,
∴∠DAB=∠DBA=30°.
∵∠C=90°,∠B=30°,∴∠CAD=∠BAD=30°.
∵DC⊥AC,DE⊥AB,∴DC=DE.
(2)解:∵DC=DE,CD=3,∴DE=3.
∵∠B=30°,DE⊥AB,∴BD=2DE=6.