2. 等邊三角形的性質(zhì):等邊三角形的三個(gè)角都
相等
,并且每一個(gè)角都等于$60^{\circ }$.
答案:相等
3. 等邊三角形的判定:三個(gè)角都
相等
的三角形是等邊三角形;有一個(gè)角是$60^{\circ }$的
等腰三角形
是等邊三角形.
答案:相等 等腰三角形
解析:
三個(gè)角都相等的三角形是等邊三角形��;有一個(gè)角是$60^{\circ }$的等腰三角形是等邊三角形.
1. 等邊三角形對(duì)稱(chēng)軸的條數(shù)是 (
C
)
A.1
B.2
C.3
D.4
答案:C
解析:
解:等邊三角形的對(duì)稱(chēng)軸是每條邊上的中線(xiàn)��、高線(xiàn)或角的平分線(xiàn)所在的直線(xiàn)��,共有3條��。
答案:C
2. 下列說(shuō)法不正確的是 (
C
)
A.三邊相等的三角形是等邊三角形
B.三個(gè)角相等的三角形是等邊三角形
C.有一個(gè)角是$60^{\circ }$的三角形是等邊三角形
D.頂角為$60^{\circ }$的等腰三角形是等邊三角形
答案:C
解析:
A. 三邊相等的三角形是等邊三角形�,正確�����。
B. 三個(gè)角相等的三角形是等邊三角形���,正確���。
C. 有一個(gè)角是$60^{\circ}$的三角形不一定是等邊三角形,錯(cuò)誤����。
D. 頂角為$60^{\circ}$的等腰三角形是等邊三角形,正確。
答案:C
3. 如圖,D,E,F分別是等邊三角形ABC各邊上的點(diǎn),且$AD= BE= CF$,則$\triangle DEF$是 (
A
)
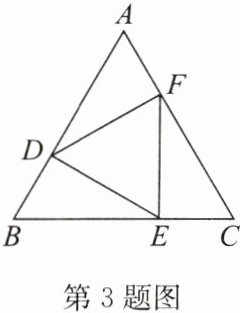
A.等邊三角形
B.腰和底邊不相等的等腰三角形
C.直角三角形
D.不等邊三角形
答案:A
解析:
解:
∵△ABC是等邊三角形����,
∴AB=BC=AC,∠A=∠B=∠C=60°.
∵AD=BE=CF���,
∴AB-AD=BC-BE=AC-CF�,即BD=CE=AF.
在△ADF�、△BED和△CFE中,
AD=BE=CF�����,∠A=∠B=∠C�,AF=BD=CE,
∴△ADF≌△BED≌△CFE(SAS).
∴DF=ED=FE.
∴△DEF是等邊三角形.
答案:A
4. (2024·黑龍江三模)如圖,直線(xiàn)$m// n,\triangle ABC$是等邊三角形,頂點(diǎn)B在直線(xiàn)n上,直線(xiàn)m交AB于點(diǎn)E,交AC于點(diǎn)F.若$∠1= 140^{\circ }$,求$∠2$的度數(shù).

答案:解:∵△ABC 是等邊三角形�����,
∴∠A=60°.
對(duì)于△AEF,∵∠1=∠A+∠AEF=140°,
∴∠AEF=140°-60°=80°,
∴∠DEB=∠AEF=80°.
∵m//n,
∴∠2+∠DEB=180°,
∴∠2=180°-80°=100°.
5. 如圖,在等邊三角形ABC的AC邊上取中點(diǎn)D,連接BD,在BC的延長(zhǎng)線(xiàn)上取一點(diǎn)E,使$CE= CD$.求證:$∠ABD= ∠E.$

答案:證明:∵△ABC 為等邊三角形,BD 是 AC 邊上的中線(xiàn)����,
∴BD⊥AC,BD 平分∠ABC,
∴∠DBE=∠ABD= $\frac{1}{2}$∠ABC=30°.
∵CD=CE,∴∠CDE=∠E.
∵∠ACB=60°,且∠ACB 為△CDE 的一個(gè)外角,
∴∠CDE+∠E=60°,∴∠CDE=∠E=30°,
∴∠ABD=∠E.