1. 如圖,已知在$\triangle ABC$中,$AB = AC$,$\angle A = 40^{\circ}$,$AB的垂直平分線交AC于點(diǎn)D$,交$AB于點(diǎn)E$,連接$BD$,則$\angle DBC$的度數(shù)為 (
A
)
A.$30^{\circ}$
B.$32^{\circ}$
C.$34^{\circ}$
D.$36^{\circ}$
答案:A
解析:
解:在$\triangle ABC$中��,$AB=AC$�,$\angle A=40^{\circ}$��,
$\therefore \angle ABC = \angle C = \frac{180^{\circ} - 40^{\circ}}{2} = 70^{\circ}$。
$\because DE$是$AB$的垂直平分線�����,
$\therefore AD = BD$����,
$\therefore \angle ABD = \angle A = 40^{\circ}$,
$\therefore \angle DBC = \angle ABC - \angle ABD = 70^{\circ} - 40^{\circ} = 30^{\circ}$�����。
答案:A
2. 等腰三角形一腰上的高與另一腰的夾角為$60^{\circ}$,則頂角的度數(shù)為 (
B
)
A.$30^{\circ}$
B.$30^{\circ}或150^{\circ}$
C.$60^{\circ}或150^{\circ}$
D.$60^{\circ}或120^{\circ}$
答案:B
解析:
解:分兩種情況討論:
情況一:等腰三角形為銳角三角形
腰上的高在三角形內(nèi)部�����,高與另一腰的夾角為$60^{\circ}$�����,則頂角為:
$90^{\circ} - 60^{\circ} = 30^{\circ}$
情況二:等腰三角形為鈍角三角形
腰上的高在三角形外部��,高與另一腰的夾角為$60^{\circ}$�,則頂角的外角為:
$90^{\circ} - 60^{\circ} = 30^{\circ}$
頂角為:$180^{\circ} - 30^{\circ} = 150^{\circ}$
綜上,頂角的度數(shù)為$30^{\circ}$或$150^{\circ}$。
答案:B
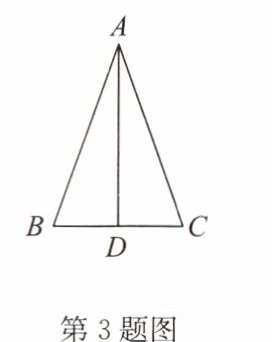
3. 如圖,在$\triangle ABC$中,$AB = AC$,$D是邊BC$的中點(diǎn),若$\angle C = 70^{\circ}$,則$\angle BAD = $
20
${}^{\circ }$.
答案:20
解析:
解:因?yàn)樵?\triangle ABC$中�����,$AB = AC$����,所以$\triangle ABC$是等腰三角形,$\angle B = \angle C = 70^{\circ}$���。
根據(jù)三角形內(nèi)角和為$180^{\circ}$����,可得$\angle BAC = 180^{\circ} - \angle B - \angle C = 180^{\circ} - 70^{\circ} - 70^{\circ} = 40^{\circ}$�。
因?yàn)?D$是邊$BC$的中點(diǎn),且$AB = AC$���,所以$AD$平分$\angle BAC$(等腰三角形三線合一)����。
因此�����,$\angle BAD = \frac{1}{2}\angle BAC = \frac{1}{2} × 40^{\circ} = 20^{\circ}$。
$20$
6. 如圖,已知$\triangle ABC$中,$AB = AC$,$AD是\angle BAC$的平分線,如果$\triangle ABD的周長(zhǎng)為12$,$\triangle ABC的周長(zhǎng)為16$,那么$AD$的長(zhǎng)是
4
.
答案:4
解析:
解:
∵AB=AC��,AD是∠BAC的平分線�����,
∴BD=CD(等腰三角形三線合一)�。
設(shè)AB=AC=x���,BD=CD=y���,AD=z。
由△ABD的周長(zhǎng)為12���,得:AB+BD+AD=12�,
即x+y+z=12 ①��。
由△ABC的周長(zhǎng)為16,得:AB+AC+BC=16�,
即2x+2y=16,化簡(jiǎn)得x+y=8 ②�。
①-②得:z=4。
∴AD的長(zhǎng)是4�����。
答案:4
7. 如圖,在$\triangle ABC$中,$AB的垂直平分線EF交BC于點(diǎn)E$,交$AB于點(diǎn)F$,$D為線段CE$的中點(diǎn),$BE = AC$.
(1)求證:$AD\perp BC$;(2)若$\angle BAC = 75^{\circ}$,求$\angle B$的度數(shù).

答案:(1)證明:連接AE,如答圖.∵EF垂直平分AB,∴AE=BE.∵BE=AC,∴AE=AC.∵D是EC的中點(diǎn),∴AD⊥BC.(2)解:設(shè)∠B=x°.∵AE=BE,∴∠BAE=∠B=x°,∴由三角形的外角的性質(zhì)得,∠AEC=2x°.∵AE=AC,∴∠C=∠AEC=2x°.在△ABC中,3x°+75°=180°,∴x°=35°,即∠B=35°.

解析:
(1)證明:連接AE�����。
∵EF垂直平分AB���,
∴AE=BE。
∵BE=AC��,
∴AE=AC����。
∵D是EC的中點(diǎn),
∴AD⊥BC�。
(2)解:設(shè)∠B=x°。
∵AE=BE����,
∴∠BAE=∠B=x°��,
∴∠AEC=∠BAE+∠B=2x°�。
∵AE=AC����,
∴∠C=∠AEC=2x°。
在△ABC中����,∠BAC+∠B+∠C=180°,
即75°+x°+2x°=180°���,
解得x=35�,
∴∠B=35°�。