1. 角的內(nèi)部到
角兩邊距離相等
的點在角的平分線上.
答案:角兩邊距離相等
如圖,∵$PD\perp OA$,$PE\perp OB$,
PD
=
PE
,
∴點 P 在$∠AOB$的平分線上.
答案:PD PE
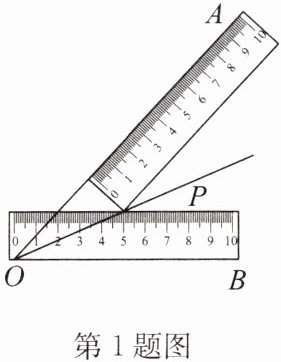
1. 兩把相同的長方形直尺按如圖所示方式擺放,記兩把直尺的接觸點為 P,其中一把直尺邊緣和射線 OA 重合,另一把直尺的下邊線與射線 OB 重合,連接 OP 并延長. 若$∠BOP = 25^{\circ}$,則$∠AOP$的度數(shù)為
(
B
)
A.$12.5^{\circ}$
B.$25^{\circ}$
C.$37.5^{\circ}$
D.$50^{\circ}$
答案:B
解析:
解:過點P分別作直尺兩邊的垂線����,垂足分別為C�、D����。
因為兩把直尺相同且為長方形,所以PC=PD�����。
所以O(shè)P是∠AOB的角平分線���。
因為∠BOP=25°�����,所以∠AOP=∠BOP=25°��。
答案:B
證明: 如圖,設(shè) AM,BN 交于點 O,過點 O 分別作$OD\perp BC$,$OE\perp AC$,$OF\perp AB$,垂足分別為 D,E,F.
∵O 是$∠BAC$的平分線 AM 上的一點(
已知
),
∴$OE = OF$(
角的平分線上的點到角的兩邊的距離相等
).
同理,$OD = OF$,
∴$OD = OE$(
等量代換
).
∵CP 是$∠ACB$的平分線(
已知
),
∴點 O 在 CP 上(
角的內(nèi)部到角兩邊距離相等的點在角的平分線上
).
因此,AM,BN,CP 交于一點.
答案:已知 角的平分線上的點到角的兩邊的距離相等 等量代換 已知 角的內(nèi)部到角兩邊距離相等的點在角的平分線上
解析:
證明: 如圖,設(shè) AM,BN 交于點 O,過點 O 分別作$OD\perp BC$,$OE\perp AC$,$OF\perp AB$,垂足分別為 D,E,F.
∵O 是$∠BAC$的平分線 AM 上的一點(已知),
∴$OE = OF$(角的平分線上的點到角的兩邊的距離相等).
同理,$OD = OF$,
∴$OD = OE$(等量代換).
∵CP 是$∠ACB$的平分線(已知),
∴點 O 在 CP 上(角的內(nèi)部到角兩邊距離相等的點在角的平分線上).
因此,AM,BN,CP 交于一點.