1.(2024·沭陽縣模擬)如圖,在$\triangle ABC$中,點(diǎn)D,E,F分別為BC,AD,CE的中點(diǎn),且$S_{\triangle ABC}= 4cm^{2}$,則陰影部分的面積為
1
$cm^{2}$.
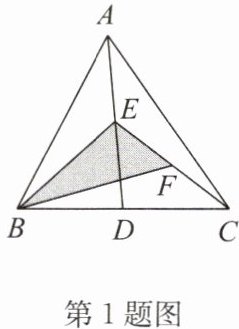
答案:1 點(diǎn)撥:由題意得△ABD��,△ACD為△ABC面積的一半����,同理可得△BEC的面積等于△ABC面積的一半,那么陰影部分的面積等于△BEC面積的一半�����。
解析:
解:
∵D是BC中點(diǎn)��,
∴S△ABD=S△ACD=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×4=2cm2��。
∵E是AD中點(diǎn)�����,
∴S△BED=$\frac{1}{2}$S△ABD=1cm2�,S△CED=$\frac{1}{2}$S△ACD=1cm2。
∴S△BEC=S△BED+S△CED=1+1=2cm2��。
∵F是CE中點(diǎn)����,
∴S△BEF=$\frac{1}{2}$S△BEC=$\frac{1}{2}$×2=1cm2���。
1
2.如圖,在$\triangle ABC$中,點(diǎn)D在邊AC上且$AD= 2CD$,E是BC的中點(diǎn),且AE,BD相交于點(diǎn)O.若$\triangle BOE$的面積為2,則$\triangle AOD$的面積為______
$\frac{16}{3}$
.
答案:1. 首先��,利用三角形面積公式$S = \frac{1}{2}ah$(等底等高的三角形面積相等):
因?yàn)?E$是$BC$的中點(diǎn)�����,根據(jù)$S_{\triangle ABE}=S_{\triangle ACE}$����,$S_{\triangle BOE}=S_{\triangle COE}$(等底$BE = CE$,同高)��。已知$S_{\triangle BOE}=2$���,所以$S_{\triangle BOC}=S_{\triangle BOE}+S_{\triangle COE}=2 + 2=4$�����。
2. 然后�,設(shè)$S_{\triangle COD}=x$:
因?yàn)?AD = 2CD$��,根據(jù)$S=\frac{1}{2}ah$(高相同,面積比等于底之比)����,則$S_{\triangle AOD}=2S_{\triangle COD}=2x$。
又因?yàn)?S_{\triangle ABD}=2S_{\triangle CBD}$($AD = 2CD$�,高相同),$S_{\triangle ABD}=S_{\triangle AOD}+S_{\triangle AOB}$���,$S_{\triangle CBD}=S_{\triangle COD}+S_{\triangle BOC}$����。
即$S_{\triangle AOD}+S_{\triangle AOB}=2(S_{\triangle COD}+S_{\triangle BOC})$�。
同時(shí),$S_{\triangle AOB}=S_{\triangle AOC}=S_{\triangle AOD}+S_{\triangle COD}=2x + x=3x$($S_{\triangle ABE}=S_{\triangle ACE}$�����,$S_{\triangle BOE}=S_{\triangle COE}$����,所以$S_{\triangle AOB}=S_{\triangle AOC}$)。
3. 最后�����,代入面積關(guān)系求解:
把$S_{\triangle AOD}=2x$,$S_{\triangle AOB}=3x$�,$S_{\triangle COD}=x$,$S_{\triangle BOC}=4$代入$S_{\triangle AOD}+S_{\triangle AOB}=2(S_{\triangle COD}+S_{\triangle BOC})$����,得到$2x+3x=2(x + 4)$。
展開方程:$5x=2x + 8$����。
移項(xiàng):$5x-2x=8$����,即$3x = 8$,$x=\frac{8}{3}$����。
則$S_{\triangle AOD}=2x$,$S_{\triangle AOD}=\frac{16}{3}$�。
故$\triangle AOD$的面積為$\frac{16}{3}$。
3.如圖,已知AD,AE分別是$\triangle ABC$的高和中線,$AB= 6cm,AC= 8cm,BC= 10cm$,$∠BAC= 90^{\circ }$.
(1)求AD的長;
(2)求$\triangle ABE$的面積;
(3)求$\triangle ACE和\triangle ABE$的周長差.

答案:1. (1)求$AD$的長:
解:因?yàn)?\angle BAC = 90^{\circ}$����,$AD$是$\triangle ABC$的高,根據(jù)三角形面積公式$S=\frac{1}{2}ah$($a$為底�,$h$為高)���,對于$\triangle ABC$,$S_{\triangle ABC}=\frac{1}{2}AB\cdot AC=\frac{1}{2}BC\cdot AD$�。
已知$AB = 6cm$,$AC = 8cm$�,$BC = 10cm$,代入$\frac{1}{2}AB\cdot AC=\frac{1}{2}BC\cdot AD$中��,可得:
$\frac{1}{2}×6×8=\frac{1}{2}×10× AD$���。
化簡得$24 = 5AD$�����,解得$AD=\frac{24}{5}=4.8cm$�����。
2. (2)求$\triangle ABE$的面積:
解:因?yàn)?AE$是$\triangle ABC$的中線���,所以$BE=\frac{1}{2}BC$(中線定義:三角形中線是連接三角形頂點(diǎn)和它的對邊中點(diǎn)的線段)。
已知$BC = 10cm$�����,則$BE=\frac{1}{2}×10 = 5cm$。
又因?yàn)?S_{\triangle ABC}=\frac{1}{2}AB\cdot AC=\frac{1}{2}×6×8 = 24cm^{2}$�,且$S_{\triangle ABE}=\frac{1}{2}S_{\triangle ABC}$(等底同高的三角形面積關(guān)系:中線將三角形分成面積相等的兩部分)。
所以$S_{\triangle ABE}=12cm^{2}$�����。
3. (3)求$\triangle ACE$和$\triangle ABE$的周長差:
解:$\triangle ACE$的周長$C_{1}=AC + CE+AE$�,$\triangle ABE$的周長$C_{2}=AB + BE+AE$。
因?yàn)?AE$是中線���,所以$CE = BE$��。
則$C_{1}-C_{2}=(AC + CE+AE)-(AB + BE+AE)$。
化簡得$C_{1}-C_{2}=AC - AB$�。
已知$AC = 8cm$,$AB = 6cm$����,所以$C_{1}-C_{2}=8 - 6=2cm$。
綜上�����,(1)$AD = 4.8cm$����;(2)$S_{\triangle ABE}=12cm^{2}$�;(3)$\triangle ACE$與$\triangle ABE$的周長差為$2cm$����。