1. 下列說法錯誤的是 (
D
)
A.等腰三角形兩腰上的高相等
B.等腰三角形兩腰上的中線相等
C.等腰三角形兩底角的平分線相等
D.等腰三角形中的高、中線和角平分線重合
答案:D
2. (2024·石家莊一模)對于題目:“在△ABC 中,AB= AC,∠ABC= 70°,分別以點 A,B 為圓心,AB 長為半徑的兩條弧相交于點 P,求∠APC 的度數(shù)”,嘉嘉求解的結果是∠APC= 80°. 淇淇說:“嘉嘉的解答正確但不全面,∠APC 還有另一個不同的值.”則下列判斷中,正確的是(
A
)
A.淇淇說得對,∠APC 的另一個值是 40°
B.淇淇說得不對,∠APC 只能等于 80°
C.嘉嘉求的結果不對,∠APC 應等于 85°
D.兩人都不對,∠APC 應有 3 個不同的值
答案:A
解析:
∵AB=AC���,∠ABC=70°,
∴∠ACB=∠ABC=70°����,∠BAC=180°-70°×2=40°。
以A���、B為圓心��,AB長為半徑畫弧交于點P�����,分兩種情況:
情況1:點P在AB下方
∵AP=AB�����,BP=AB��,
∴AP=BP=AB�����,△ABP為等邊三角形����,∠BAP=60°。
∵AC=AB=AP��,
∴△APC為等腰三角形�,∠CAP=∠BAP-∠BAC=60°-40°=20°�����。
∠APC=(180°-∠CAP)/2=(180°-20°)/2=80°����。
情況2:點P在AB上方
同理△ABP為等邊三角形,∠BAP=60°���,∠CAP=∠BAC+∠BAP=40°+60°=100°�����。
△APC為等腰三角形����,∠APC=(180°-∠CAP)/2=(180°-100°)/2=40°。
綜上�����,∠APC=80°或40°�����,淇淇說得對����,另一個值是40°。
A
3. 等腰三角形一腰上的高與另一腰的夾角為 30°,則底角的度數(shù)為
$60^{\circ}$或$30^{\circ}$
.
答案:$60^{\circ}$或$30^{\circ}$
4. 如圖,在△ABC 中,AB= AC,點 D,E 分別在邊 BC,AB 上,AD= DE. 如果∠CAD= 60°,∠BDE= 15°,那么∠C 的度數(shù)是
$35^{\circ}$
.
答案:$35^{\circ}$
解析:
設∠C = x
∵AB = AC
∴∠B = ∠C = x����,∠BAC = 180° - 2x
∵∠CAD = 60°
∴∠BAD = ∠BAC - ∠CAD = 180° - 2x - 60° = 120° - 2x
∵AD = DE
∴∠AED = ∠BAD = 120° - 2x
∠BED = 180° - ∠AED = 180° - (120° - 2x) = 60° + 2x
在△BDE中,∠B + ∠BDE + ∠BED = 180°
即x + 15° + (60° + 2x) = 180°
3x + 75° = 180°
3x = 105°
x = 35°
∠C = 35°
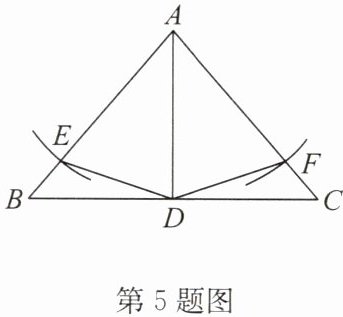
5. 如圖,在△ABC 中,AB= AC,AD 為△ABC 的角平分線. 以點 A 為圓心,AD 長為半徑畫弧,與 AB,AC 分別交于點 E,F,連接 DE,DF.
(1)求證:△ADE≌△ADF;
(2)若∠BAC= 80°,求∠BDE 的度數(shù).
答案:
(1)證明:
∵AD是△ABC的角平分線����,
∴∠BAD = ∠CAD.由作圖知:AE = AF.在△ADE和△ADF中�����,$\begin{cases}AE = AF\\\angle EAD = \angle FAD\\AD = AD\end{cases}$
∴△ADE≌△ADF(SAS).
(2)解:
∵∠BAC = 80°���,AD為△ABC的角平分線,
∴∠EAD = $\frac{1}{2}$∠BAC = 40°.由作圖知:AE = AD����,
∴∠AED = ∠ADE,
∴∠ADE = $\frac{1}{2}$×(180° - 40°) = 70°.
∵AB = AC�,AD為△ABC的角平分線,
∴AD⊥BC.
∴∠BDE = 90° - ∠ADE = 20°.
6. 如圖,在△ABC 中,AB= AC,∠BAC= 50°,∠BAC 的平分線與 AB 的垂直平分線交于點 O. 若沿 EF 折疊后點 C 與點 O 重合,則∠CEF 的度數(shù)是 (
C
)
A.60°
B.55°
C.50°
D.45°
答案:C
解析:
連接BO����,CO。
∵AB=AC��,∠BAC=50°����,AO平分∠BAC����,
∴∠BAO=∠CAO=25°���,∠ABC=∠ACB=(180°-50°)/2=65°。
∵DO垂直平分AB���,
∴OA=OB���,∠OBA=∠BAO=25°,∠OBC=65°-25°=40°���。
∵AB=AC��,∠BAO=∠CAO�,AO=AO����,
∴△ABO≌△ACO(SAS),OB=OC�,∠OCA=∠OBC=40°,∠OCE=65°-40°=25°��。
∵折疊后點C與O重合,
∴EF垂直平分OC����,∠OEF=∠CEF,∠OFE=90°�����,∠EOC=∠OCE=25°�,∠CEF=90°-25°=65°-40°=25°+30°=55°。
答案:B
7. 如圖,在△ABC 中,AB= AC,點 D,E 分別在 AB,AC 邊上,DB= DE= AE,BE= BC,則∠BAC 的度數(shù)為
$45^{\circ}$
.
答案:$45^{\circ}$
解析:
設∠BAC = $ x $�����。
∵ $ AE = DE $����,
∴ ∠ADE = ∠BAC = $ x $,
∴ ∠AED = $ 180^\circ - 2x $����,
∴ ∠DEB = $ 180^\circ - (180^\circ - 2x) = 2x $。
∵ $ DB = DE $��,
∴ ∠DBE = ∠DEB = $ 2x $�,
∴ ∠BDE = $ 180^\circ - 2 × 2x = 180^\circ - 4x $。
∵ ∠ADB = $ 180^\circ $����,
∴ ∠ADE + ∠BDE = $ 180^\circ $,即 $ x + (180^\circ - 4x) = 180^\circ $���,解得 $ x = 0^\circ $(舍去��,不合題意)���。
重新推導∠DEB:∠AED = $ 180^\circ - 2x $,∠DEB = $ 180^\circ - ∠AED = 2x $(正確)�。
∠ADB為平角,∠ADE = $ x $���,∠BDE = $ 180^\circ - x - ∠EDC $(錯誤����,應為∠ADB = ∠ADE + ∠EDB = $ 180^\circ $���,即∠EDB = $ 180^\circ - x $)����。
∵ $ DB = DE $,
∴ ∠DBE = ∠DEB = $ y $�����,則∠EDB = $ 180^\circ - 2y $�����,
∴ $ 180^\circ - 2y = 180^\circ - x $�,得 $ x = 2y $,即 $ y = \frac{x}{2} $����,∠DEB = $ \frac{x}{2} $。
∠AEB = ∠AED + ∠DEB = $ (180^\circ - 2x) + \frac{x}{2} = 180^\circ - \frac{3x}{2} $��。
AB = AC��,∠ABC = ∠ACB = $ \frac{180^\circ - x}{2} $�����。
BE = BC����,∠BEC = ∠BCE = ∠ACB = $ \frac{180^\circ - x}{2} $��。
∠AEB + ∠BEC = $ 180^\circ $�����,
$ 180^\circ - \frac{3x}{2} + \frac{180^\circ - x}{2} = 180^\circ $,
$ 180^\circ - \frac{3x}{2} + 90^\circ - \frac{x}{2} = 180^\circ $�����,
$ 270^\circ - 2x = 180^\circ $�,
$ 2x = 90^\circ $,
$ x = 45^\circ $�。
∠BAC = $ 45^\circ $
$ 45^\circ $
8. 如圖,在△ABC 中,AB= AC,∠ABC= 30°,D,E 分別為 BC,AB 邊上的動點,且∠ADE= 45°. 若△ADE 為等腰三角形,則∠DAC 的大小為
30°
.
答案:1. 首先,因為$AB = AC$�,$\angle ABC=30^{\circ}$,根據(jù)等腰三角形性質$\angle C=\angle B = 30^{\circ}$���,再由三角形內角和定理$\angle BAC=180^{\circ}-\angle B-\angle C$���,可得:
$\angle BAC = 180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}$。
2. 然后���,因為$\triangle ADE$為等腰三角形���,分三種情況討論:
情況一:當$AD = AE$時:
則$\angle AED=\angle ADE = 45^{\circ}$�,根據(jù)三角形內角和定理$\angle DAE=180^{\circ}-\angle ADE - \angle AED$����,可得$\angle DAE=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}$。
又因為$\angle BAC = 120^{\circ}$���,所以$\angle DAC=\angle BAC-\angle DAE$���,即$\angle DAC = 120^{\circ}-90^{\circ}=30^{\circ}$。
情況二:當$DA = DE$時:
則$\angle DAE=\angle AED$�,根據(jù)三角形外角性質$\angle AED=\angle B+\angle BDE$,設$\angle BDE=x$����,則$\angle AED=\angle DAE = 30^{\circ}+x$。
在$\triangle ADE$中����,由三角形內角和定理$\angle DAE+\angle AED+\angle ADE = 180^{\circ}$,即$(30^{\circ}+x)+(30^{\circ}+x)+45^{\circ}=180^{\circ}$���。
化簡方程:$2x+105^{\circ}=180^{\circ}$����,$2x=180^{\circ}-105^{\circ}=75^{\circ}$,解得$x = 37.5^{\circ}$����。
所以$\angle DAE=30^{\circ}+37.5^{\circ}=67.5^{\circ}$,則$\angle DAC=\angle BAC-\angle DAE=120^{\circ}-67.5^{\circ}=52.5^{\circ}$(舍去���,因為$D$,$E$是動點�����,這種情況不符合圖形的實際情況)���。
情況三:當$EA = ED$時:
則$\angle EAD=\angle ADE = 45^{\circ}$�,所以$\angle DAC=\angle BAC-\angle DAE$��,即$\angle DAC = 120^{\circ}-45^{\circ}=75^{\circ}$(舍去��,因為$D$���,$E$是動點�,這種情況不符合圖形的實際情況)。
綜上����,$\angle DAC$的大小為$30^{\circ}$。
解析:
在△ABC中�,AB=AC,∠ABC=30°�,則∠BAC=120°,∠C=30°�����。
情況1:AD=AE
∠ADE=∠AED=45°����,∠DAE=90°,∠DAC=∠BAC-∠DAE=120°-90°=30°���。
情況2:AD=DE
∠DAE=∠DEA=(180°-45°)/2=67.5°�����,∠DAC=∠BAC-∠DAE=120°-67.5°=52.5°��。
情況3:AE=DE
∠DAE=∠ADE=45°�����,∠DAC=∠BAC-∠DAE=120°-45°=75°�。
綜上,∠DAC的大小為$30^{\circ}$或$52.5^{\circ}$或$75^{\circ}$����。