1. 閱讀教材第 118 頁閱讀與思考,解決下列問題:
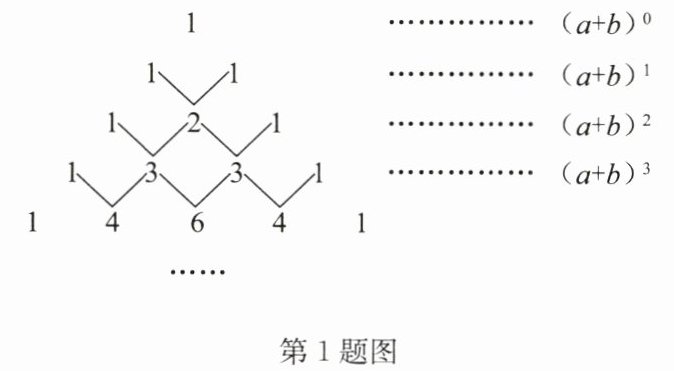
“楊輝三角”(如圖)的構(gòu)造法則為:兩腰上的數(shù)都是 1,其余每個數(shù)均為它上方左右兩數(shù)之和.事實上,這個三角形給出了$(a + b)^n(n = 0,1,2,3,…)$的展開式(按$a$的次數(shù)由大到小的順序排列)的系數(shù)規(guī)律.例如,在三角形中第三行的三個數(shù) 1,2,1,恰好對應(yīng)$(a + b)^2 = a^2 + 2ab + b^2$展開式中各項的系數(shù);第四行的四個數(shù) 1,3,3,1,恰好對應(yīng)$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$展開式中各項的系數(shù);等等.
根據(jù)上面的規(guī)律,請你解答下列問題.
(1)計算:$(a + b)^0 = $
1
;$(a + b\neq0)$
(2)若$(a + b)^4 = a^4 + ma^3b + na^2b^2 + 4ab^3 + b^4$(m,n 是常數(shù)),則$m = $
4
,n =
6
;
(3)若$(a + b)^5 = a^5 + xa^4b + 10a^3b^2 + ya^2b^3 + 5ab^4 + b^5$(x,y 是常數(shù)),則$x = $
5
,y =
10
;
(4)求式子$7^5 - 5×7^4×5 + 10×7^3×5^2 + 10×7^2×(-125) + 5×7×(-5)^4 - 5^5$的值.
解:由(3)可得$(a+b)^{5}=a^{5}+5a^{4}b+10a^{3}b^{2}+10a^{2}b^{3}+5ab^{4}+b^{5}$,
$\therefore 7^{5}-5×7^{4}×5+10×7^{3}×5^{2}+10×7^{2}×(-125)+5×7×(-5)^{4}-5^{5}$
$=7^{5}+5×7^{4}×(-5)+10×7^{3}×(-5)^{2}+10×7^{2}×(-5)^{3}+5×7×(-5)^{4}+(-5)^{5}$
$=[7+(-5)]^{5}$
$=2^{5}$
$=32.$