10. (8分)計(jì)算下列各式:
(1)$(3x - 2y)(6x - 4y)$;
(2)$(a + b)(3a - 2b)-b(a - b)$;
(3)$(y + 2)(y - 2)-(y - 1)(y + 5)$;
(4)$(a - b)(a^{2}+ab + b^{2})$.
答案:【解析】:
本題主要考察了多項(xiàng)式乘法的分配律和合并同類項(xiàng)的知識點(diǎn)。
對于每一個(gè)小式,都需要使用分配律進(jìn)行展開���,然后合并同類項(xiàng)進(jìn)行化簡���。
(1)對于$(3x - 2y)(6x - 4y)$�,可以將其視為$3x$乘以$6x - 4y$減去$2y$乘以$6x - 4y$��,然后合并同類項(xiàng)���。
(2)對于$(a + b)(3a - 2b)-b(a - b)$��,首先分別展開$(a + b)(3a - 2b)$和$b(a - b)$�,然后相減并合并同類項(xiàng)����。
(3)對于$(y + 2)(y - 2)-(y - 1)(y + 5)$����,首先分別展開$(y + 2)(y - 2)$和$(y - 1)(y + 5)$���,然后相減并合并同類項(xiàng)。
(4)對于$(a - b)(a^{2}+ab + b^{2})$����,可以直接應(yīng)用分配律進(jìn)行展開,然后合并同類項(xiàng)��。
【答案】:
(1)解:
$(3x - 2y)(6x - 4y)$
$= 3x \cdot 6x + 3x \cdot (-4y) + (-2y) \cdot 6x + (-2y) \cdot (-4y)$
$= 18x^{2} - 12xy - 12xy + 8y^{2}$
$= 18x^{2} - 24xy + 8y^{2}$
(2)解:
$(a + b)(3a - 2b)-b(a - b)$
$= a \cdot 3a + a \cdot (-2b) + b \cdot 3a + b \cdot (-2b) - ab + b^{2}$
$= 3a^{2} - 2ab + 3ab - 2b^{2} - ab + b^{2}$
$= 3a^{2} - b^{2}$
(3)解:
$(y + 2)(y - 2)-(y - 1)(y + 5)$
$= y^{2} - 2y + 2y - 4 - (y^{2} + 5y - y - 5)$
$= y^{2} - 4 - y^{2} - 4y + 5$
$= - 4y + 1$
(4)解:
$(a - b)(a^{2}+ab + b^{2})$
$= a \cdot a^{2} + a \cdot ab + a \cdot b^{2} - b \cdot a^{2} - b \cdot ab - b \cdot b^{2}$
$= a^{3} + a^{2}b + ab^{2} - a^{2}b - ab^{2} - b^{3}$
$= a^{3} - b^{3}$
11. (12分)已知$2^{a}= 3$,$2^����= 5$,$2^{c}= 75$.
(1)求$2^{2a}$的值;
(2)求$2^{c - b + a}$的值.
答案:(1)解:因?yàn)?2^{a}=3$,根據(jù)冪的乘方公式$(2^{a})^{2}=2^{2a}$��,所以$2^{2a}=3^{2}=9$��。
(2)解:因?yàn)?2^{a}=3$����,$2^=5$����,$2^{c}=75$,根據(jù)同底數(shù)冪的乘除法則,$2^{c - b + a}=2^{c}÷2^�����×2^{a}$�����,所以$2^{c - b + a}=75÷5×3=15×3=45$��。
12. (12分)先化簡,再求值:$(2x + y)^{2}-(2x + y)(2x - y)-2y(x + y)$,其中$x = (\frac{1}{2})^{2023}$,$y = 2^{2022}$.
答案:解:原式$=4x^{2}+4xy+y^{2}-(4x^{2}-y^{2})-2xy-2y^{2}$
$=4x^{2}+4xy+y^{2}-4x^{2}+y^{2}-2xy-2y^{2}$
$=2xy$
當(dāng)$x=(\frac{1}{2})^{2023}$��,$y=2^{2022}$時(shí)�����,
原式$=2×(\frac{1}{2})^{2023}×2^{2022}$
$=2×(\frac{1}{2}×2)^{2022}×\frac{1}{2}$
$=2×1^{2022}×\frac{1}{2}$
$=2×1×\frac{1}{2}$
$=1$
13. (12分)(2024春·姜堰區(qū)期末)如圖,長方形ABCD的面積為$S_{1}$,三角形EFG的面積為$S_{2}$($m>2$).
(1)分別求出$S_{1}與S_{2}$的值(結(jié)果用含m的代數(shù)式表示,并化為最簡形式).
(2)若一個(gè)正方形的邊長為$3m + 4$,設(shè)該正方形的面積為$S_{3}$,試探究:$S_{3}與3(S_{1}+S_{2})$的差是否是定值?若是定值,請求出該值;若不是定值,請說明理由.
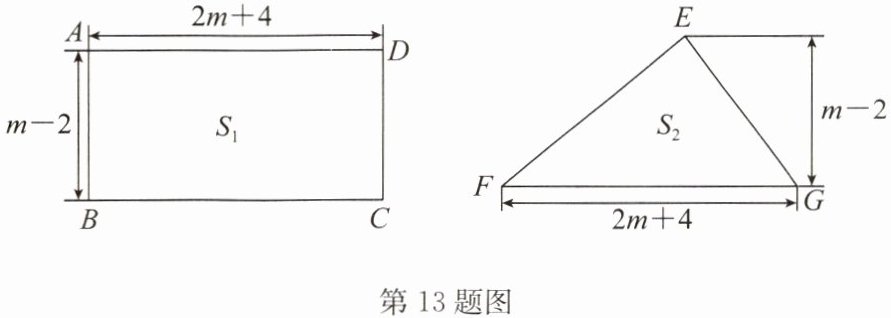
答案:【解析】:(1)根據(jù)題意����,長方形ABCD的長為$2m+4$,寬為$m-2$���,
所以$S_1=(2m+4)(m-2)$
$=2m^2-4m+4m-8$
$=2m^2-8$
三角形EFG的底為$2m+4$��,高為$m-2$��,
所以$S_2=\frac{1}{2}×(2m+4)(m-2)$
$=\frac{1}{2}×(2m^2-4m+4m-8)$
$=(m^2-4)$
(2)根據(jù)題意���,正方形的邊長為$3m+4$,
所以$S_3=(3m+4)^2$
$=9m^2+24m+16$
計(jì)算$3(S_1+S_2)$的值��,
$3(S_1+S_2)=3×[(2m^2-8)+(m^2-4)]$
$=3×(3m^2-12)$
$=9m^2-36$
計(jì)算$S_3$與$3(S_1+S_2)$的差�,
$S_3-3(S_1+S_2)=(9m^2+24m+16)-(9m^2-36)$
$=24m+52$
由于差中含有變量m,且m的系數(shù)不為0��,所以差不是定值����。
【答案】:(1)$S_1=2m^2-8$,$S_2=m^2-4$
(2)$S_3-3(S_1+S_2)$不是定值