10.(12分)計(jì)算:
(1)$48^{\circ}39' + 67^{\circ}31'$; (2)$\frac{11}{5}×(-\frac{1}{3} - \frac{1}{2})×\frac{9}{11}÷(-\frac{3}{2})^{2}$.
答案:解:(1)原式=115°70′=116°10′.
(2)原式=$\frac{11}{5}×(-\frac{5}{6})×\frac{9}{11}÷\frac{9}{4}=-\frac{3}{2}×\frac{4}{9}=-\frac{2}{3}$.
11.(10分)先化簡(jiǎn),再求值:$2a^{2} - 5a + 2 - 6a^{2} + 6a - 3$,其中$a = -1$.
答案:解:原式=-4a2+a-1,
把a(bǔ)=-1代入得,
原式=-4×(-1)2+(-1)-1=-6.
12.(14分)為了支持國(guó)貨,某手機(jī)賣場(chǎng)本月計(jì)劃用9萬元購進(jìn)某國(guó)產(chǎn)品牌手機(jī),從賣場(chǎng)獲知該品牌3種不同型號(hào)的手機(jī)進(jìn)價(jià)及售價(jià)如下表:
|手機(jī)型號(hào)|A|B|C|
|進(jìn)價(jià)/(元/部)|1500|2100|2500|
|售價(jià)/(元/部)|1650|2300|2750|
若該手機(jī)賣場(chǎng)同時(shí)購進(jìn)兩種不同型號(hào)的手機(jī)共50臺(tái),9萬元?jiǎng)偤糜猛?
(1)請(qǐng)你確定該手機(jī)賣場(chǎng)的進(jìn)貨方案,并說明理由;
(2)該賣場(chǎng)老板準(zhǔn)備把這批手機(jī)銷售利潤(rùn)的50%捐給公益組織,在同時(shí)購進(jìn)兩種不同型號(hào)手機(jī)的方案中,為了使捐款最多,你選擇哪種方案?
答案:解:(1)①當(dāng)購進(jìn)A和B兩種型號(hào)手機(jī)時(shí),
設(shè)購進(jìn)A型手機(jī)a臺(tái),則購進(jìn)B型號(hào)手機(jī)(50-a)臺(tái),
根據(jù)題意得1500a+2100(50-a)=90000,解得a=25,
故可購進(jìn)A型手機(jī)25臺(tái),購進(jìn)B型號(hào)手機(jī)25臺(tái).
②當(dāng)購進(jìn)B和C兩種型號(hào)手機(jī)時(shí),
設(shè)購進(jìn)B型號(hào)手機(jī)b臺(tái),則購進(jìn)C型號(hào)手機(jī)(50-b)臺(tái),
根據(jù)題意得2100b+2500(50-b)=90000,
解得b=87.5>50,故舍去.
③當(dāng)購進(jìn)A和C兩種型號(hào)手機(jī)時(shí),
設(shè)購進(jìn)C型號(hào)手機(jī)c臺(tái),則購進(jìn)A型號(hào)手機(jī)(50-c)臺(tái),
根據(jù)題意得1500(50-c)+2500c=90000,解得c=15,
故可購進(jìn)C型號(hào)手機(jī)15臺(tái),購進(jìn)A型手機(jī)35臺(tái).
故有兩種進(jìn)貨方案.
方案一:可購進(jìn)A型手機(jī)25臺(tái),購進(jìn)B型號(hào)手機(jī)25臺(tái);
方案二:可購進(jìn)C型號(hào)手機(jī)15臺(tái),購進(jìn)A型手機(jī)35臺(tái).
(2)方案一的利潤(rùn):25×(1650-1500)+25×(2300-2100)=8750(元),捐款數(shù)額:8750×50%=4375(元);
方案二的利潤(rùn):15×(2750-2500)+35×(1650-1500)=9000(元),捐款數(shù)額:9000×50%=4500(元).
因?yàn)?375<4500,
故選擇方案二,即購進(jìn)C型號(hào)手機(jī)15臺(tái),購進(jìn)A型手機(jī)35臺(tái),可以使捐款最多.
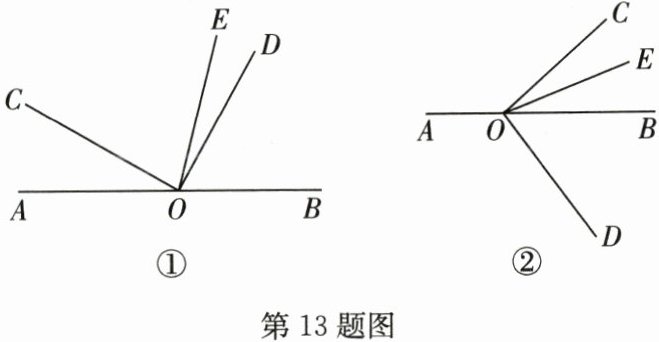
13.(19分)點(diǎn)O是直線AB上一點(diǎn),$∠COD$是直角,OE平分$∠BOC$.
(1)①如圖①,若$∠DOE = 15^{\circ}$,求$∠AOC$的度數(shù);
②如圖②,若$∠DOE = \alpha$,求$∠AOC$的度數(shù).(用含α的式子表示)
(2)將圖①中的$∠COD$繞點(diǎn)O按順時(shí)針方向旋轉(zhuǎn)至圖②所示的位置.探究$∠DOE與∠AOC$之間的數(shù)量關(guān)系,寫出你的結(jié)論,并說明理由.
答案:解:(1)①因?yàn)椤螩OD=90°,∠DOE=15°,
所以∠COE=∠COD-∠DOE=90°-15°=75°.
又因?yàn)镺E平分∠BOC,
所以∠BOC=2∠COE=150°,
所以∠AOC=180°-∠BOC=180°-150°=30°.
②因?yàn)椤螩OD=90°,∠DOE=α,
所以∠COE=∠COD-∠DOE=90°-α.
又因?yàn)镺E平分∠BOC,
所以∠BOC=2∠COE=180°-2α,
所以∠AOC=180°-∠BOC=180°-(180°-2α)=2α.
(2)∠DOE=$\frac{1}{2}$∠AOC,理由如下:
因?yàn)镺E平分∠BOC,
所以∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(180°-∠AOC)=90°-$\frac{1}{2}$∠AOC.
又因?yàn)椤螩OD=90°,
所以∠DOE=90°-∠COE=90°-(90°-$\frac{1}{2}$∠AOC)=$\frac{1}{2}$∠AOC.