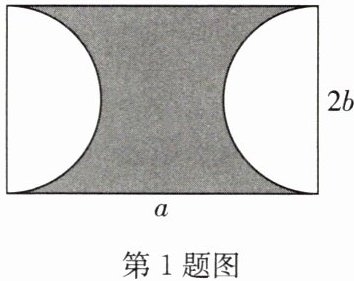
1. (2024 秋·嵩縣期末)如圖,長方形的長為 $ a $,寬為 $ 2b $.
(1)用含 $ a $, $ b $ 的代數(shù)式表示圖中陰影部分的面積 $ S $;
(2)當(dāng) $ a = 5 \text{cm} $, $ b = 2 \text{cm} $ 時,求陰影部分的面積 $ S $ 的值. ($ \pi $ 取 3.14)
答案:1.解:(1)因?yàn)殚L方形的長為a,寬為2b,所以$ S_{陰影}=2ab-\pi b^{2} $.(2)當(dāng)$ a=5cm,b=2cm $時,$ S_{陰影}=2× 5× 2-3.14× 4=7.44(cm^{2}) $,即陰影部分的面積S的值是$ 7.44cm^{2} $.
解析:
(1)長方形的面積為長乘寬���,即$a×2b = 2ab$�。由圖可知��,兩個空白部分可組成一個直徑為$2b$的圓�����,其半徑為$b$��,面積為$\pi b^2$�����。所以陰影部分面積$S=2ab-\pi b^2$�。
(2)當(dāng)$a = 5\,\text{cm}$����,$b = 2\,\text{cm}$時���,$S=2×5×2-3.14×2^2$
$=20 - 3.14×4$
$=20 - 12.56$
$=7.44\,\text{cm}^2$。
即陰影部分面積$S$的值是$7.44\,\text{cm}^2$����。
2. 如圖是由長為 4、寬為 3 的長方形與邊長為 $ x(x < 3) $ 的正方形拼成的圖形.
(1)當(dāng) $ x = 2 $ 時,求陰影部分的面積;
(2)用含 $ x $ 的代數(shù)式表示圖中陰影部分的面積,并化簡.

答案:2.解:(1)當(dāng)$ x=2 $時,陰影部分的面積為$ 2× 2+4× 3-\frac{1}{2}× 2× 2-\frac{1}{2}× 3× (2+4)-\frac{1}{2}× 4× (3-2)=4+12-2-9-2=3 $.(2)陰影部分的面積為$ x^{2}+4× 3-\frac{1}{2}x^{2}-\frac{1}{2}× 3× (x+4)-\frac{1}{2}× 4× (3-x)=x^{2}+12-\frac{1}{2}x^{2}-\frac{3}{2}x-6-6+2x=\frac{1}{2}x^{2}+\frac{1}{2}x $.
3. (2024 秋·海門區(qū)期中)如圖,在長方形中剪下兩個大小相同的正方形(有關(guān)線段的長如圖所示),留下一個“T”形圖形(陰影部分).
(1)用含 $ x $, $ y $ 的代數(shù)式表示“T”形圖形的面積,并化簡;
(2)已知 $ y = 3x = 12 \text{m} $,在“T”形區(qū)域鋪上單價為 20 元/$ \text{m}^2 $ 的草坪,請計(jì)算草坪的造價.

答案:3.解:(1)"T"形圖形的面積為$ 2(x+y+x+y)+xy=2xy+2x^{2}+2xy+xy=2x^{2}+5xy $.(2)因?yàn)? y=3x=12m $,所以$ x=4m,y=12m $.所以草坪的造價為$ (2× 4^{2}+5× 4× 12)× 20=5440 $(元).
解析:
(1)長方形的長為$y + x + y = x + 2y$�����,寬為$2x + y$�����,面積為$(x + 2y)(2x + y)$�。兩個正方形的邊長均為$y$,面積和為$2y^2$���?!癟”形圖形的面積為長方形面積減去兩個正方形面積����,即$(x + 2y)(2x + y)-2y^2$,展開化簡得$2x^2+5xy$。
(2)因?yàn)?y = 12\,\text{m}$�,$3x = 12\,\text{m}$,所以$x = 4\,\text{m}$���。將$x = 4$����,$y = 12$代入$2x^2 + 5xy$�,得$2×4^2+5×4×12 = 272\,\text{m}^2$���。草坪造價為$272×20 = 5440$元�����。
(1)$2x^2 + 5xy$
(2)$5440$元