15. 如圖是一個(gè)數(shù)值運(yùn)算的程序,若輸出y的值為40,則輸入的x的值為
9 或 -9
.
答案:9 或 -9
解析:
解:根據(jù)程序可得運(yùn)算式為$y = \frac{x^2 - 1}{2}$�����。
已知輸出$y = 40$�,則:
$\frac{x^2 - 1}{2} = 40$
$x^2 - 1 = 80$
$x^2 = 81$
$x = \pm 9$
答案:9 或 -9
16. 如圖,在數(shù)軸上豎直擺放一個(gè)直徑為4個(gè)單位長度的半圓,A是半圓弧的中點(diǎn),半圓直徑的一個(gè)端點(diǎn)位于原點(diǎn)O.該半圓沿?cái)?shù)軸從原點(diǎn)O開始向右無滑動(dòng)滾動(dòng),當(dāng)點(diǎn)A第一次落在數(shù)軸上時(shí),此時(shí)點(diǎn)A表示的數(shù)為
4 + π
.
答案:$ 4 + \pi $
解析:
解:半圓直徑為4,半徑為2��。初始時(shí)���,半圓直徑端點(diǎn)在原點(diǎn)O���,A為半圓弧中點(diǎn),位于直徑上方。
半圓無滑動(dòng)滾動(dòng)�,當(dāng)A第一次落在數(shù)軸上時(shí),半圓需滾動(dòng)半周��。
滾動(dòng)過程中��,圓心水平移動(dòng)距離等于半圓周長的一半�,即$\frac{1}{2} × \pi × 4 = 2\pi$。但此時(shí)A點(diǎn)軌跡為以圓心為頂點(diǎn)的圓弧�����,當(dāng)滾動(dòng)半周后����,A點(diǎn)從初始位置(圓心正上方)旋轉(zhuǎn)180°至圓心正下方���,此時(shí)A點(diǎn)到初始原點(diǎn)O的距離為:直徑長度(4)加上圓心移動(dòng)距離的一半(因?yàn)闈L動(dòng)半周�,圓心移動(dòng)距離為半圓周長的一半$2\pi$��,但此時(shí)A點(diǎn)相對(duì)于圓心的水平位移為0��,水平總距離為初始直徑長度4)�。
故點(diǎn)A表示的數(shù)為$4 + \pi$。
答案:$4 + \pi$
17. 如圖,用含a的代數(shù)式表示圖中陰影部分的面積為
$\frac{1}{2}\pi a^2 - a^2$
.(結(jié)果保留π)
答案:$ \frac{1}{2}\pi a^2 - a^2 $ 解析:觀察題圖可得, 陰影部分的面積等于兩個(gè)半徑為 $ a $ 的四分之一圓的面積的和減去邊長為 $ a $ 的正方形的面積, 即陰影部分的面積為 $ 2 × \frac{1}{4} × \pi × a^2 - a^2 = \frac{1}{2}\pi a^2 - a^2 $.
解析:
解:陰影部分的面積為兩個(gè)半徑為 $a$ 的四分之一圓的面積之和減去邊長為 $a$ 的正方形的面積。
兩個(gè)四分之一圓的面積和為:$2×\frac{1}{4}×\pi× a^2=\frac{1}{2}\pi a^2$
正方形的面積為:$a^2$
所以陰影部分面積為:$\frac{1}{2}\pi a^2 - a^2$
$\frac{1}{2}\pi a^2 - a^2$
18. (揚(yáng)州中考)將黑色圓點(diǎn)按如圖所示的規(guī)律進(jìn)行排列:
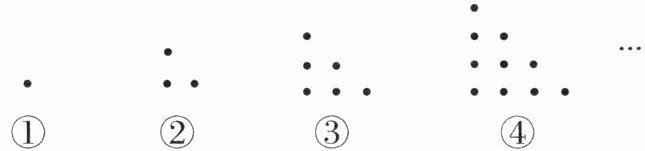
圖中黑色圓點(diǎn)的個(gè)數(shù)依次為1,3,6,10,…,將其中所有能被3整除的數(shù)按從小到大的順序重新排列成一組新數(shù)據(jù),則新數(shù)據(jù)中的第33個(gè)數(shù)為______
1275
.
答案:1 275 解析:題圖①②③④中的黑色圓點(diǎn)的個(gè)數(shù)分別為 1, 3, 6, 10, 所以第 $ n $ 個(gè)圖形中的黑色圓點(diǎn)的個(gè)數(shù)為 $ \frac{n(n + 1)}{2} $, 所以這列數(shù)為 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, …, 其中每 3 個(gè)數(shù)中, 后 2 個(gè)數(shù)能被 3 整除, $ 33 ÷ 2 = 16 \cdots 1 $, $ 16 × 3 + 2 = 50 $, 則第 33 個(gè)能被 3 整除的數(shù)為原數(shù)列中第 50 個(gè)數(shù), 即 $ \frac{50 × 51}{2} = 1 275 $. 故答案為 1 275.
解析:
解:第$n$個(gè)圖形中黑色圓點(diǎn)的個(gè)數(shù)為$\frac{n(n + 1)}{2}$����。
原數(shù)列:1,3�����,6��,10����,15,21�����,28����,36,45��,55�,66,78,91�,…
觀察可知,每3個(gè)數(shù)中后2個(gè)數(shù)能被3整除�����。
$33÷2 = 16\cdots\cdots1$��,則原數(shù)列中對(duì)應(yīng)的項(xiàng)數(shù)為$16×3 + 2=50$���。
第50個(gè)數(shù)為$\frac{50×51}{2}=1275$����。
故答案為1275���。
$19. (10$分$)$計(jì)算:
$(1)(-3) + (-4) - (+11) - (-9)��;$$(2)-1^{100} + (-\frac{1}{8} + \frac{1}{3} - \frac{1}{6})×(-24);$
$(3)1\frac{1}{2}×\frac{5}{7} - (-\frac{5}{7})×2\frac{1}{2} + (-\frac{1}{2})÷1\frac{2}{5}���;$$(4)-199\frac{5}{7}×14($要求用簡便方法計(jì)算$)��;$$(5)-4^2×\frac{5}{8} - |-5|×(-4)^3×\frac{1}{4} + 2^2÷4.$
答案:
(1)-9
(2)-2
(3)$ \frac{5}{2} $
(4)-2 796
(5)71
解析:
(1)解:原式=-3-4-11+9=-18+9=-9
(2)解:原式$=-1+(-\frac{1}{8})×(-24)+\frac{1}{3}×(-24)-\frac{1}{6}×(-24)=-1+3-8+4=-2$
(3)解:原式$=\frac{3}{2}×\frac{5}{7}+\frac{5}{7}×\frac{5}{2}-\frac{1}{2}×\frac{5}{7}=\frac{5}{7}×(\frac{3}{2}+\frac{5}{2}-\frac{1}{2})=\frac{5}{7}×\frac{7}{2}=\frac{5}{2}$
(4)解:原式$=(-200+\frac{2}{7})×14=-200×14+\frac{2}{7}×14=-2800+4=-2796$
(5)解:原式$=-16×\frac{5}{8}-5×(-64)×\frac{1}{4}+4÷4=-10+80+1=71$
20. (6分)先化簡,再求值:$(1)2x^2 - [3(-\frac{1}{3}x^2 + \frac{2}{3}xy) + 2y^2] - 2(x^2 - xy - 2y^2),其中x = \frac{1}{2},$y = -1����;
(2)已知a + b = 4,ab = -2,求$(4a - 3b + 2ab) - 2(a - \frac{5}{2}b - ab)$的值.
答案:(1)原式 $ = 2 x ^ { 2 } - ( - x ^ { 2 } + 2 x y + 2 y ^ { 2 } ) - 2 ( x ^ { 2 } - x y - 2 y ^ { 2 } ) = 2 x ^ { 2 } + x ^ { 2 } - 2 x y - 2 y ^ { 2 } - 2 x ^ { 2 } + 2 x y + 4 y ^ { 2 } = x ^ { 2 } + 2 y ^ { 2 } $, 當(dāng) $ x = \frac{1}{2} $, $ y = -1 $ 時(shí), 原式 $ = ( \frac{1}{2} ) ^ { 2 } + 2 × ( - 1 ) ^ { 2 } = \frac{1}{4} + 2 = \frac{9}{4} $. (2) $ ( 4 a - 3 b + 2 a b ) - 2 ( a - \frac{5}{2} b - a b ) = 4 a - 3 b + 2 a b - 2 a + 5 b + 2 a b = 2 a + 2 b + 4 a b = 2 ( a + b ) + 4 a b $, 當(dāng) $ a + b = 4 $, $ a b = - 2 $ 時(shí), 原式 $ = 2 × 4 + 4 × ( - 2 ) = 0 $.
解析:
(1)解:原式$=2x^2 - [3(-\frac{1}{3}x^2 + \frac{2}{3}xy) + 2y^2] - 2(x^2 - xy - 2y^2)$
$=2x^2 - (-x^2 + 2xy + 2y^2) - 2x^2 + 2xy + 4y^2$
$=2x^2 + x^2 - 2xy - 2y^2 - 2x^2 + 2xy + 4y^2$
$=x^2 + 2y^2$
當(dāng)$x = \frac{1}{2}$,$y = -1$時(shí)���,原式$=(\frac{1}{2})^2 + 2×(-1)^2 = \frac{1}{4} + 2 = \frac{9}{4}$
(2)解:$(4a - 3b + 2ab) - 2(a - \frac{5}{2}b - ab)$
$=4a - 3b + 2ab - 2a + 5b + 2ab$
$=2a + 2b + 4ab$
$=2(a + b) + 4ab$
當(dāng)$a + b = 4$���,$ab = -2$時(shí),原式$=2×4 + 4×(-2) = 8 - 8 = 0$