1. 當(dāng)$x= -1$時(shí),代數(shù)式$2x^{2}-5x$的值為 (
D
)
A.5
B.3
C.-2
D.7
答案:D
解析:
當(dāng)$x = -1$時(shí)�,
$2x^{2}-5x = 2×(-1)^{2}-5×(-1)$
$=2×1 + 5$
$=2 + 5$
$=7$
D
2. (2025·長沙期中)攝氏度與華氏度是兩種常用的溫度計(jì)量單位,它們之間的轉(zhuǎn)換關(guān)系滿足方程$F= \frac {9}{5}C+32$,其中F表示華氏度($^{\circ }F$),C表示攝氏度($^{\circ }C$),那么將$25^{\circ }C$轉(zhuǎn)換為華氏度為 (
A
)
A.$77^{\circ }F$
B.$82^{\circ }F$
C.$86^{\circ }F$
D.$91^{\circ }F$
答案:A
解析:
解:將$C = 25$代入$F=\frac{9}{5}C + 32$,得
$F=\frac{9}{5}×25+32$
$=45 + 32$
$=77$
答案:A
3. 當(dāng)$x= 2與x= -2$時(shí),代數(shù)式$x^{4}-2x^{2}+3$的兩個(gè)值 (
A
)
A.相等
B.互為倒數(shù)
C.互為相反數(shù)
D.無法比較大小
答案:A
解析:
當(dāng)$x = 2$時(shí)����,$x^{4}-2x^{2}+3=2^{4}-2×2^{2}+3=16 - 8 + 3=11$;
當(dāng)$x=-2$時(shí)�,$x^{4}-2x^{2}+3=(-2)^{4}-2×(-2)^{2}+3=16 - 8 + 3=11$。
兩個(gè)值相等�����。
A
4. (1)(岳陽中考)已知$x-3= 2$,則代數(shù)式$(x-3)^{2}-2(x-3)+1$的值為
1
.
(2)若$a^{2}-4a-12= 0$,則$2a^{2}-8a-8$的值為
16
.
(3)已知$y= x-1$,則$(x-y)^{2}+(y-x)+1$的值為
1
.
答案:(1)1 (2)16 (3)1
解析:
(1)解:因?yàn)?x - 3 = 2$,所以原式$=2^{2}-2×2 + 1=4 - 4 + 1=1$
(2)解:因?yàn)?a^{2}-4a - 12 = 0$���,所以$a^{2}-4a=12$�,原式$=2(a^{2}-4a)-8=2×12 - 8=24 - 8=16$
(3)解:因?yàn)?y=x - 1$����,所以$x - y=1$,原式$=1^{2}+(-1)+1=1 - 1 + 1=1$
5. 教材P83習(xí)題T6變式 請(qǐng)先設(shè)計(jì)計(jì)算$(x-2)^{2}+3$的值的計(jì)算程序,再計(jì)算并填寫下表:
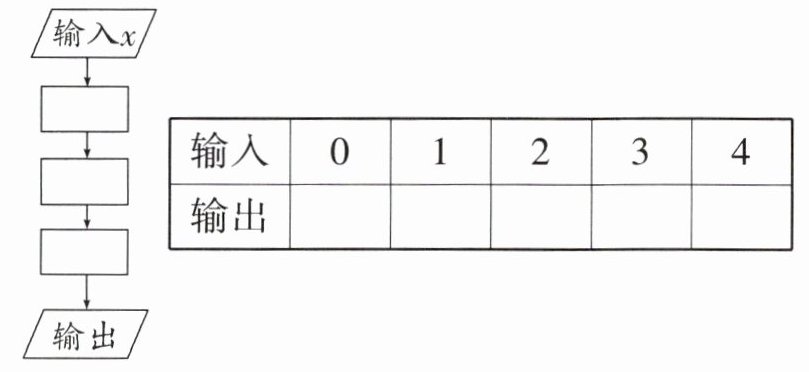
?2 平方 +3 7 4 3 4 7
答案:?2 平方 +3 7 4 3 4 7(合理即可)
解析:
計(jì)算程序:輸入x→減去2→平方→加上3→輸出�。
輸入 | 0 | 1 | 2 | 3 | 4
---|---|---|---|---|---
輸出 | 7 | 4 | 3 | 4 | 7
6. 當(dāng)$x= 3,y= -\frac {1}{2}$時(shí),求下列代數(shù)式的值:
(1)$2x^{2}-4xy^{2}+4y$; (2)$\frac {x^{2}+4xy}{2xy-y^{2}}$.
答案:(1)13 (2)$-\frac{12}{13}$
解析:
(1)解:當(dāng)$x = 3$,$y=-\frac{1}{2}$時(shí)����,
$\begin{aligned}&2x^{2}-4xy^{2}+4y\\=&2×3^{2}-4×3×\left(-\frac{1}{2}\right)^{2}+4×\left(-\frac{1}{2}\right)\\=&2×9 - 12×\frac{1}{4}-2\\=&18 - 3 - 2\\=&13\end{aligned}$
(2)解:當(dāng)$x = 3$,$y=-\frac{1}{2}$時(shí)��,
$\begin{aligned}&\frac{x^{2}+4xy}{2xy-y^{2}}\\=&\frac{3^{2}+4×3×\left(-\frac{1}{2}\right)}{2×3×\left(-\frac{1}{2}\right)-\left(-\frac{1}{2}\right)^{2}}\\=&\frac{9 - 6}{-3-\frac{1}{4}}\\=&\frac{3}{-\frac{13}{4}}\\=&-\frac{12}{13}\end{aligned}$
7. 如圖所示.
(1)用代數(shù)式表示長方形ABCD中陰影部分的面積;
(2)當(dāng)$a= 10,b= 4$時(shí),求陰影部分的面積.(其中$π\(zhòng)approx 3.14$)

答案:(1)陰影部分的面積為$ab - 2×\frac{1}{4}×πb^{2} = ab - \frac{1}{2}πb^{2}$�。(2)當(dāng)$a = 10$,$b = 4$時(shí)�����,$ab - \frac{1}{2}πb^{2} ≈ 10×4 - \frac{1}{2}×3.14×16 = 14.88$��。
解析:
(1)陰影部分的面積為長方形面積減去兩個(gè)四分之一圓的面積�����,即$ab - 2×\frac{1}{4}\pi b^2 = ab - \frac{1}{2}\pi b^2$。
(2)當(dāng)$a = 10$�,$b = 4$時(shí),代入上式可得:$10×4 - \frac{1}{2}×3.14×4^2 = 40 - \frac{1}{2}×3.14×16 = 40 - 25.12 = 14.88$���。
8. (2025·大連期末)無論x取何值,下列代數(shù)式的值一定是負(fù)數(shù)的是 (
D
)
A.-x
B.-|x|
C.$-x^{2}$
D.$-x^{2}-1$
答案:D 解析:$|x|$和$x^{2}$均為非負(fù)數(shù)�,故$-x^{2} - 1$一定是負(fù)數(shù)�����,故選D��。
9. 已知當(dāng)$x= 2025$時(shí),代數(shù)式$ax^{3}+bx-3$的值是2,當(dāng)$x= -2025$時(shí),代數(shù)式$ax^{3}+bx+7$的值等于 (
C
)
A.-10
B.4
C.2
D.-6
答案:C 解析:因?yàn)楫?dāng)$x = 2025$時(shí)����,代數(shù)式$ax^{3} + bx - 3$的值是2���,所以$2025^{3}a + 2025b = 5$��。當(dāng)$x = -2025$時(shí)����,代數(shù)式$ax^{3} + bx + 7 = (-2025)^{3}a - 2025b + 7 = -(2025^{3}a + 2025b) + 7 = -5 + 7 = 2$。故選C�����。
10. 若a是最大的負(fù)整數(shù),b是絕對(duì)值最小的有理數(shù),c是倒數(shù)等于它本身的自然數(shù),則代數(shù)式$a^{2025}+2026b+c^{2025}$的值為
0
.
答案:0 解析:由題意知$a = -1$�����,$b = 0$����,$c = 1$,所以$a^{2025} + 2026b + c^{2025} = (-1)^{2025} + 2026×0 + 1^{2025} = 0$��。
解析:
解:由題意知:
$a = -1$(最大的負(fù)整數(shù))��,
$b = 0$(絕對(duì)值最小的有理數(shù))�����,
$c = 1$(倒數(shù)等于它本身的自然數(shù))�����。
則代數(shù)式的值為:
$\begin{aligned}a^{2025} + 2026b + c^{2025}&=(-1)^{2025} + 2026×0 + 1^{2025}\\&=-1 + 0 + 1\\&=0\end{aligned}$
答案:0
11. (1)按圖中的程序計(jì)算,若輸出的值為-1,則輸入的數(shù)為
14
.
(2)如圖是一個(gè)數(shù)值轉(zhuǎn)換機(jī).若輸出的結(jié)果為10,則輸入a的值為
±4
.
答案:(1)14 (2)$\pm 4$