8.隨著服裝市場(chǎng)競(jìng)爭(zhēng)日益激烈,某品牌服裝專賣店一款服裝按原售價(jià)降價(jià)a元后,再打7折,現(xiàn)售價(jià)為b元,則原售價(jià)為(
B
)
A.$(a + \frac{7b}{10})$元
B.$(a + \frac{10b}{7})$元
C.$(b + \frac{7a}{10})$元
D.$(b + \frac{10a}{7})$元
答案:B 解析:由題意可得,原售價(jià)為 $b÷0.7 + a = b×\frac{10}{7} + a = \left(a + \frac{10b}{7}\right)$ 元����,故選 B。
9.某城市按以下規(guī)定收取每月的煤氣費(fèi):用氣不超過(guò)$60m^{3}$,按每立方米0.8元收費(fèi);如果超過(guò)$60m^{3}$,超過(guò)部分每立方米按1.2元收費(fèi).已知某戶用煤氣$x m^{3}(x > 60)$,則該戶應(yīng)交煤氣費(fèi)
(1.2x - 24)
元.
答案:(1.2x - 24) 解析:因?yàn)槌?$60m^3$ 的煤氣用量為 $(x - 60)m^3$����,所以超出的費(fèi)用是 $1.2(x - 60) = (1.2x - 72)$ 元��,所以應(yīng)交煤氣費(fèi)是 $1.2x - 72 + 60×0.8 = (1.2x - 24)$ 元�����。故答案為 $(1.2x - 24)$�����。
解析:
解:因?yàn)?$ x > 60 $�,所以煤氣費(fèi)分為兩部分:
不超過(guò) $ 60m^3 $ 的費(fèi)用:$ 60×0.8 = 48 $ 元�����;
超過(guò) $ 60m^3 $ 的部分為 $ (x - 60)m^3 $�����,費(fèi)用:$ 1.2(x - 60) = 1.2x - 72 $ 元�����。
應(yīng)交總煤氣費(fèi):$ 48 + (1.2x - 72) = 1.2x - 24 $ 元。
故答案為 $ (1.2x - 24) $��。
10.(1)觀察一列數(shù):$-\frac{1}{2},\frac{3}{4},-\frac{5}{6},\frac{7}{8},…$.按此規(guī)律,這一列數(shù)的第n個(gè)數(shù)是
$(-1)^n\cdot\frac{2n - 1}{2n}$
.
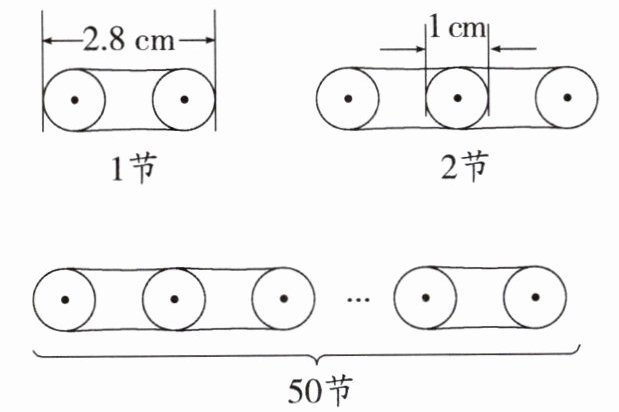
(2)如圖,某鏈條每節(jié)長(zhǎng)為2.8cm,每?jī)晒?jié)鏈條相連接部分重疊的圓的直徑為1cm,按這種連接方式,50節(jié)鏈條總長(zhǎng)度為
91
cm,n節(jié)鏈條總長(zhǎng)度為
$(1.8n + 1)$
cm.
答案:(1) $(-1)^n\cdot\frac{2n - 1}{2n}$
(2) $91$ $(1.8n + 1)$ 解析:$1$ 節(jié)鏈條的長(zhǎng)度是 $2.8cm$�,之后每多 $1$ 節(jié)鏈條,鏈條總長(zhǎng)變長(zhǎng) $2.8 - 1 = 1.8(cm)$�����,$1$ 節(jié)鏈條可視為 $1 + 1.8 = 2.8(cm)$�����,$2$ 節(jié)鏈條可視為 $1 + 1.8×2 = 4.6(cm)$����,以此類推����,故 $50$ 節(jié)鏈條總長(zhǎng)度為 $1 + 1.8×50 = 91(cm)$,$n$ 節(jié)鏈條總長(zhǎng)度為 $1 + 1.8× n = (1.8n + 1)cm$�����。
11.甲�����、乙、丙三家超市為了促銷一種定價(jià)均為$m(m > 0)$元的商品,都進(jìn)行了兩次價(jià)格下調(diào),降價(jià)情況如表所示:
| |甲超市|乙超市|丙超市|
|第一次降價(jià)|20%|25%|30%|
|第二次降價(jià)|20%|15%|10%|
那么顧客到哪家超市購(gòu)買(mǎi)這種商品最劃算?請(qǐng)通過(guò)計(jì)算加以說(shuō)明.
答案:降價(jià)后三家超市的售價(jià):甲為 $(1 - 20\%)(1 - 20\%)m = 0.64m$(元)��,乙為 $(1 - 25\%)(1 - 15\%)m = 0.6375m$(元)��,丙為 $(1 - 30\%)(1 - 10\%)m = 0.63m$(元)����。因?yàn)?$0.63m < 0.6375m < 0.64m$,所以顧客到丙超市購(gòu)買(mǎi)這種商品最劃算���。
12.觀察下列等式:
①$\frac{3}{2} = \frac{1}{1} + \frac{1}{2}$;②$\frac{3}{5} = \frac{1}{2} + \frac{1}{10}$;③$\frac{3}{8} = \frac{1}{3} + \frac{1}{24}$;
④$\frac{3}{11} = \frac{1}{4} + \frac{1}{44}……$
根據(jù)上述等式的規(guī)律,解答下列問(wèn)題:
(1)寫(xiě)出第5個(gè)等式:
$\frac{3}{14} = \frac{1}{5} + \frac{1}{70}$
;
(2)寫(xiě)出第n個(gè)等式(n為正整數(shù)):
$\frac{3}{3n - 1} = \frac{1}{n} + \frac{1}{n(3n - 1)}$
(用含有n的式子表示);
(3)應(yīng)用你發(fā)現(xiàn)的規(guī)律,計(jì)算:$\frac{3}{5} + \frac{3}{17} + \frac{3}{35} - \frac{1}{10} - \frac{1}{102} - \frac{1}{420} = $
$\frac{3}{4}$
.
答案:(1) $\frac{3}{14} = \frac{1}{5} + \frac{1}{70}$ (2) $\frac{1}{3n - 1} = \frac{1}{n} + \frac{1}{n(3n - 1)}$
(3) $\frac{3}{4}$ 解析:$\frac{3}{5} + \frac{3}{17} + \frac{3}{35} - \frac{1}{10} - \frac{1}{102} - \frac{1}{420} = \frac{1}{2} + \frac{1}{10} + \frac{1}{6} + \frac{1}{102} + \frac{1}{12} + \frac{1}{420} - \frac{1}{10} - \frac{1}{102} - \frac{1}{420} = \frac{1}{2} + \frac{1}{6} + \frac{1}{12} = \frac{3}{4}$�����。
13.【問(wèn)題背景】在$\triangle ABC$內(nèi)部,有點(diǎn)$P_{1}$,可構(gòu)成3個(gè)不重疊的小三角形(如圖①).
【探究發(fā)現(xiàn)】當(dāng)$\triangle ABC$內(nèi)的點(diǎn)的個(gè)數(shù)增加時(shí)(見(jiàn)圖①~③),探究三角形內(nèi)互不重疊的小三角形的個(gè)數(shù)情況.

(1)填表:
|三角形內(nèi)點(diǎn)的個(gè)數(shù)n|1|2|3|4|…|
|不重疊三角形的個(gè)數(shù)S|
3
|
5
|
7
|
9
|…|
(2)當(dāng)$\triangle ABC$內(nèi)部有n個(gè)點(diǎn)($P_{1},P_{2},…,P_{n}$)時(shí),三角形內(nèi)不重疊的小三角形的個(gè)數(shù)$S = 2025$,求n的值.
根據(jù)(1)的規(guī)律���,當(dāng)$\triangle ABC$內(nèi)部有$n$個(gè)點(diǎn)($P_1,P_2,\cdots,P_n$)時(shí),可以把$\triangle ABC$分割成$S = 2n + 1$個(gè)互不重疊的三角形����,當(dāng)$S = 2025$時(shí),$2n + 1 = 2025$��,所以$n = 1012$。
答案:(1) $3$ $5$ $7$ $9$ 解析:如題圖①中�,當(dāng) $\triangle ABC$ 內(nèi)只有 $1$ 個(gè)點(diǎn)時(shí),可分割成 $3$ 個(gè)互不重疊的小三角形;題圖②中�,當(dāng) $\triangle ABC$ 內(nèi)只有 $2$ 個(gè)點(diǎn)時(shí),可分割成 $5$ 個(gè)互不重疊的小三角形;題圖③中����,當(dāng) $\triangle ABC$ 內(nèi)只有 $3$ 個(gè)點(diǎn)時(shí)����,可分割成 $7$ 個(gè)互不重疊的小三角形;同理得����,當(dāng) $\triangle ABC$ 內(nèi)只有 $4$ 個(gè)點(diǎn)時(shí)�����,可分割成 $9$ 個(gè)互不重疊的小三角形����。故答案為 $3,5,7,9$。
(2) 根據(jù) (1) 的規(guī)律��,當(dāng) $\triangle ABC$ 內(nèi)部有 $n$ 個(gè)點(diǎn) ($P_1,P_2,\cdots,P_n$) 時(shí),可以把 $\triangle ABC$ 分割成 $S = 2n + 1$ 個(gè)互不重疊的三角形�����,當(dāng) $S = 2025$ 時(shí)��,$2n + 1 = 2025$��,所以 $n = 1012$�����。