1. 數(shù)軸上的兩個(gè)點(diǎn)表示的數(shù)為-3與a,并且$a > -3$,它們之間的距離可以表示為 (
D
)
A.$3 - a$
B.$-3 - a$
C.$a - 3$
D.$a + 3$
答案:D
解析:
解:數(shù)軸上兩點(diǎn)之間的距離等于這兩個(gè)點(diǎn)表示的數(shù)的差的絕對(duì)值�����。已知兩個(gè)點(diǎn)表示的數(shù)為-3與a,且a>-3��,所以它們之間的距離為|a - (-3)| = |a + 3|����。因?yàn)閍>-3,所以a + 3>0�,|a + 3| = a + 3���。
答案:D
2. 我們知道,若在數(shù)軸上,點(diǎn)A,B分別表示數(shù)a,b,則A,B之間的距離為$|a - b|$,已知點(diǎn)A,B,C,D,在數(shù)軸上分別表示數(shù)a,b,c,d,且$|a - c| = |b - c| = \frac{3}{2}|d - a| = 3(a ≠ b)$,則點(diǎn)C,D間的距離為_(kāi)___.
答案:5 或 1 解析:因?yàn)閨a - c| = |b - c| = 3,所以點(diǎn) C 在點(diǎn) A 和點(diǎn) B 之間.因?yàn)?\frac{3}{2}|d - a| = 3$,所以|d - a| = 2,不妨設(shè)點(diǎn) A 在點(diǎn) B 左側(cè),如圖①:

點(diǎn) C,D 間的距離為 5;如圖②:

點(diǎn) C,D 間的距離為 1.綜上所述:點(diǎn) C,D 間的距離為 5 或 1.
3. 已知數(shù)軸上有A,B兩點(diǎn),它們對(duì)應(yīng)的數(shù)分別為1和-2.5,解答下面的問(wèn)題:
(1)觀察數(shù)軸,與點(diǎn)A的距離為4的點(diǎn)表示的數(shù)是
5 或-3
;
(2)數(shù)軸上有點(diǎn)C,且點(diǎn)C到點(diǎn)B的距離是點(diǎn)A到點(diǎn)B的距離的2倍,則點(diǎn)C表示的數(shù)是
4.5 或-9.5
;
(3)若將數(shù)軸折疊,使得點(diǎn)A與表示-3的點(diǎn)重合,求與點(diǎn)B重合的點(diǎn)表示的數(shù).
因?yàn)辄c(diǎn) A 到表示-3 的點(diǎn)的距離為|1 - (-3)| = 4,所以點(diǎn) A 到折疊點(diǎn)的距離為 2,所以折疊點(diǎn)表示的數(shù)為-1,點(diǎn) B 到表示-1 的點(diǎn)的距離為|-2.5 - (-1)| = 1.5,$-1 + 1.5 = 0.5$,所以與點(diǎn) B 重合的點(diǎn)表示的數(shù)是 0.5.
答案:(1)5 或-3
(2)4.5 或-9.5 解析:點(diǎn) A 到點(diǎn) B 的距離為|1 - (-2.5)| = 3.5,所以點(diǎn) C 到點(diǎn) B 的距離為 7,$-2.5 - 7 = -9.5$,$-2.5 + 7 = 4.5$,故點(diǎn) C 表示的數(shù)為 4.5 或-9.5.
(3)因?yàn)辄c(diǎn) A 到表示-3 的點(diǎn)的距離為|1 - (-3)| = 4,所以點(diǎn) A 到折疊點(diǎn)的距離為 2,所以折疊點(diǎn)表示的數(shù)為-1,點(diǎn) B 到表示-1 的點(diǎn)的距離為|-2.5 - (-1)| = 1.5,$-1 + 1.5 = 0.5$,所以與點(diǎn) B 重合的點(diǎn)表示的數(shù)是 0.5.
4. 數(shù)軸上點(diǎn)M表示有理數(shù)-3,將點(diǎn)M向右平移2個(gè)單位長(zhǎng)度到達(dá)點(diǎn)N,點(diǎn)E到點(diǎn)N的距離為4,則點(diǎn)E表示的有理數(shù)為 (
B
)
A.3
B.-5或3
C.-9或-1
D.-1
答案:B
解析:
解:點(diǎn)M表示-3,向右平移2個(gè)單位得點(diǎn)N��,
點(diǎn)N表示的數(shù)為:-3 + 2 = -1���。
設(shè)點(diǎn)E表示的數(shù)為x����,
∵點(diǎn)E到點(diǎn)N的距離為4����,
∴|x - (-1)| = 4,即|x + 1| = 4���。
當(dāng)x + 1 = 4時(shí)�,x = 3���;
當(dāng)x + 1 = -4時(shí)�,x = -5���。
點(diǎn)E表示的有理數(shù)為-5或3����。
答案:B
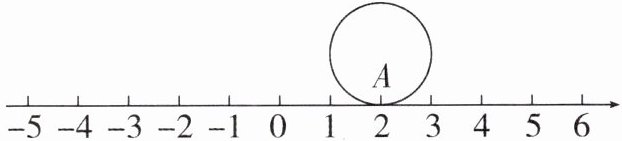
5. (2025·韶關(guān)期中)如圖,直徑為2的圓上有一點(diǎn)A,且點(diǎn)A與數(shù)軸上表示2的點(diǎn)重合,將這個(gè)圓在數(shù)軸上向左無(wú)滑動(dòng)的滾動(dòng),當(dāng)點(diǎn)A再次與數(shù)軸上的某個(gè)點(diǎn)重合時(shí),這個(gè)點(diǎn)的位置可能在 (
D
)
A.8與9之間
B.7與8之間
C.-4與-3之間
D.-5與-4之間
答案:D 解析:因?yàn)檫@個(gè)圓在數(shù)軸上無(wú)滑動(dòng)的滾動(dòng),所以滾動(dòng)一周行進(jìn)的距離為圓的周長(zhǎng)(向左或者向右的距離).因?yàn)樵搱A的直徑為 2,所以周長(zhǎng)為$πd = π×2 = 2π$,所以將這個(gè)圓在數(shù)軸上向左無(wú)滑動(dòng)的滾動(dòng),當(dāng)點(diǎn) A 再次與數(shù)軸上的某個(gè)點(diǎn)重合時(shí),這個(gè)點(diǎn)可能為$2 - 2π$,因?yàn)?-5 < 2 - 2π < -4$,所以這個(gè)點(diǎn)的位置可能在-5 與-4 之間.故選 D.
6. 數(shù)軸上,點(diǎn)A的初始位置表示的數(shù)為2,現(xiàn)點(diǎn)A做如下移動(dòng):第1次點(diǎn)A向左移動(dòng)1個(gè)單位長(zhǎng)度至點(diǎn)$A_1$,第2次從點(diǎn)$A_1$向右移動(dòng)2個(gè)單位長(zhǎng)度至點(diǎn)$A_2$,第3次從點(diǎn)$A_2$向左移動(dòng)3個(gè)單位長(zhǎng)度至點(diǎn)$A_3$,…,按照這種移動(dòng)方式進(jìn)行下去,點(diǎn)$A_{2025}$表示的數(shù)是
-1011
.
答案:-1011 解析:第 n 次移動(dòng) n 個(gè)單位長(zhǎng)度���,則第 2025 次向左移動(dòng)$2025×1$個(gè)單位長(zhǎng)度��,每左移右移各一次后��,點(diǎn) A 右移 1 個(gè)單位長(zhǎng)度,所以$A_{2025}$表示的數(shù)是$2 + 1×(2024÷2) - 2025 = -1011$.
解析:
解:第1次移動(dòng)后�����,點(diǎn)$A_1$表示的數(shù)為$2 - 1 = 1$�����;
第2次移動(dòng)后�,點(diǎn)$A_2$表示的數(shù)為$1 + 2 = 3$����;
第3次移動(dòng)后��,點(diǎn)$A_3$表示的數(shù)為$3 - 3 = 0$��;
第4次移動(dòng)后,點(diǎn)$A_4$表示的數(shù)為$0 + 4 = 4$�����;
……
觀察規(guī)律���,每?jī)纱我苿?dòng)(一左一右)為一個(gè)循環(huán)�,右移$2 - 1 = 1$個(gè)單位長(zhǎng)度��,循環(huán)結(jié)束后點(diǎn)表示的數(shù)為$2 + 1×k$($k$為循環(huán)次數(shù))����。
因?yàn)?2025$為奇數(shù),前$2024$次移動(dòng)共$2024÷2 = 1012$個(gè)循環(huán)�,此時(shí)點(diǎn)表示的數(shù)為$2 + 1×1012 = 1014$。
第$2025$次為向左移動(dòng)$2025$個(gè)單位長(zhǎng)度����,所以點(diǎn)$A_{2025}$表示的數(shù)是$1014 - 2025 = -1011$。
答案:$-1011$
7. 點(diǎn)A,B,C,D在數(shù)軸上的位置如圖所示,已知點(diǎn)C,D之間的距離為2,點(diǎn)B,C之間的距離為5,點(diǎn)A,C之間的距離是點(diǎn)C,D之間距離的6倍.

(1)若點(diǎn)C為原點(diǎn),則點(diǎn)A表示的數(shù)是____
-12
.
(2)若點(diǎn)P,Q分別從A,D兩點(diǎn)同時(shí)出發(fā),點(diǎn)P沿?cái)?shù)軸正方向以每秒3個(gè)單位長(zhǎng)度的速度向右運(yùn)動(dòng),到達(dá)點(diǎn)C后立即按原速向點(diǎn)A折返;點(diǎn)Q沿?cái)?shù)軸負(fù)方向以每秒1個(gè)單位長(zhǎng)度的速度向左運(yùn)動(dòng).當(dāng)P,Q中的某點(diǎn)到達(dá)點(diǎn)A時(shí),兩點(diǎn)同時(shí)停止運(yùn)動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為t(單位:s).
①當(dāng)$t = 3$時(shí),點(diǎn)P與點(diǎn)Q之間的距離為_(kāi)___
2
;
②當(dāng)$t = $____
$\frac{7}{2}$或5
時(shí),點(diǎn)P與點(diǎn)Q相遇.
答案:(1)-12 解析:因?yàn)辄c(diǎn) C,D 之間的距離為 2,點(diǎn) A,C 之間的距離是點(diǎn) C,D 之間距離的 6 倍,所以點(diǎn) A,C 之間的距離是 12.因?yàn)辄c(diǎn) C 為原點(diǎn),所以點(diǎn) A 表示的數(shù)是-12.
(2)①2 解析:因?yàn)辄c(diǎn) A,C 之間的距離是 12,$12÷3 = 4(s)$,所以點(diǎn) P 經(jīng)過(guò) 4s 到達(dá)點(diǎn) C,當(dāng)$t = 3$時(shí),點(diǎn) A,P 之間的距離是 9,點(diǎn) A,D 之間的距離是 14,所以此時(shí)點(diǎn) A,Q 之間的距離是$14 - 1×3 = 11$,所以點(diǎn) P 與點(diǎn) Q 之間的距離為$11 - 9 = 2$.
②$\frac{7}{2}$ 或 5 解析:當(dāng)$t < 4$或$t = 4$時(shí),點(diǎn) A,P 之間的距離是 3t,點(diǎn) A,Q 之間的距離是$14 - t$,當(dāng)$3t = 14 - t$時(shí),點(diǎn) P 與點(diǎn) Q 相遇,得$t = \frac{7}{2}$;當(dāng)$4 < t < 8$或$t = 8$時(shí),點(diǎn) A,P 之間的距離是$24 - 3t$,點(diǎn) A,Q 之間的距離是$14 - t$,當(dāng)$24 - 3t = 14 - t$時(shí),點(diǎn) P 與點(diǎn) Q 相遇,得$t = 5$.綜上,$t = \frac{7}{2}$或 5 時(shí),點(diǎn) P 與點(diǎn) Q 相遇.