亚洲激情+欧美激情,无码任你躁久久久久久,我的极品美女老婆,性欧美牲交在线视频,亚洲av高清在线一区二区三区

零五網(wǎng) › 全部參考答案› 經(jīng)綸學(xué)典學(xué)霸 › 2025年學(xué)霸題中題七年級數(shù)學(xué)上冊蘇科版 第42頁解析答案
8. 若$|6 - x|與|y + 9|$互為相反數(shù),則$x = $
6
,$y = $
-9
.
答案：6 -9
解析：
解：因?yàn)閨6 - x|與|y + 9|互為相反數(shù)，所以|6 - x| + |y + 9| = 0。
又因?yàn)榻^對值具有非負(fù)性，即|6 - x| ≥ 0，|y + 9| ≥ 0，所以只有當(dāng)|6 - x| = 0且|y + 9| = 0時(shí)等式成立。
則6 - x = 0，解得x = 6；y + 9 = 0，解得y = -9。
x = 6，y = -9。
9. (1)當(dāng)$x = $
3
時(shí),$|x - 3| + 5$有最小值,為
5
.
(2)當(dāng)$x = $
$-\frac{1}{2}$
時(shí),$9 - |x + \frac{1}{2}|$有最大值,為
9
.
答案：(1)3 5 (2)$-\frac{1}{2}$ 9
解析：
(1)因?yàn)榻^對值具有非負(fù)性，即$|x - 3| \geq 0$，當(dāng)且僅當(dāng)$x - 3 = 0$，即$x = 3$時(shí)，$|x - 3|$取得最小值$0$。所以當(dāng)$x = 3$時(shí)，$|x - 3| + 5$有最小值，最小值為$0 + 5 = 5$。
(2)因?yàn)?|x + \frac{1}{2}| \geq 0$，所以$-|x + \frac{1}{2}| \leq 0$，當(dāng)且僅當(dāng)$x + \frac{1}{2} = 0$，即$x = -\frac{1}{2}$時(shí)，$-|x + \frac{1}{2}|$取得最大值$0$。所以當(dāng)$x = -\frac{1}{2}$時(shí)，$9 - |x + \frac{1}{2}|$有最大值，最大值為$9 + 0 = 9$。
(1)3；5
(2)$-\frac{1}{2}$；9
10. 已知$|xy - 2|與|y - 1|$互為相反數(shù),試求$\frac{1}{xy} + \frac{1}{(x + 1)(y + 1)} + \frac{1}{(x + 2)(y + 2)} + … + \frac{1}{(x + 2025)(y + 2025)}$的值.


答案：由題意得$|xy - 2| + |y - 1| = 0$,所以$xy = 2$,$y = 1$,所以$x = 2$,則原式=$\frac{1}{1×2} + \frac{1}{2×3} + \frac{1}{3×4} + \cdots + \frac{1}{2026×2027} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \cdots + \frac{1}{2026} - \frac{1}{2027} = 1 - \frac{1}{2027} = \frac{2026}{2027}$.
解析：
解：由題意得$|xy - 2| + |y - 1| = 0$，
因?yàn)榻^對值為非負(fù)數(shù)，所以$xy - 2 = 0$且$y - 1 = 0$，
解得$y = 1$，代入$xy = 2$得$x = 2$。
則原式$=\frac{1}{2×1} + \frac{1}{(2+1)(1+1)} + \frac{1}{(2+2)(1+2)} + \cdots + \frac{1}{(2+2025)(1+2025)}$
$=\frac{1}{1×2} + \frac{1}{2×3} + \frac{1}{3×4} + \cdots + \frac{1}{2026×2027}$
$=1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \cdots + \frac{1}{2026} - \frac{1}{2027}$
$=1 - \frac{1}{2027}$
$=\frac{2026}{2027}$。
答案：$\frac{2026}{2027}$
11. (2025·武漢校級月考)【定義新知】
我們知道:式子$|x - 3|$的幾何意義是數(shù)軸上表示有理數(shù)x的點(diǎn)與表示有理數(shù)3的點(diǎn)之間的距離,因此,若點(diǎn)A,B在數(shù)軸上分別表示有理數(shù)a,b,則A,B兩點(diǎn)之間的距離$AB = |a - b|$.若點(diǎn)P表示的數(shù)為x,請根據(jù)數(shù)軸解決以下問題:
(1)若$|x + 5| = 6$,則x的值為
1或-11
.
(2)當(dāng)$|x + 3| + |x - 1|$取最小值時(shí),x可以取整數(shù)
-3,-2,-1,0,1
;$|x + 3| - |x - 1|$的最大值為
4
.
(3)當(dāng)$x = $
-2
時(shí),$|x + 2| + |x + 6| + |x - 1|$的值最小,最小值為
7
.
(4)如圖,一條筆直的公路邊有三個(gè)居民區(qū)A,B,C和市民廣場O,居民區(qū)A,B,C分別位于市民廣場左側(cè)5km,右側(cè)1km,右側(cè)3km.A居民區(qū)有居民1000人,B居民區(qū)有居民2000人,C居民區(qū)有居民3000人.現(xiàn)因物流需要,需要在該公路上建菜鳥驛站,用于接收這3個(gè)小區(qū)的快遞,若快遞的運(yùn)輸成本為1元/(千份·千米),那么菜鳥驛站建在何處才能使總運(yùn)輸成本最低,最低成本是多少?

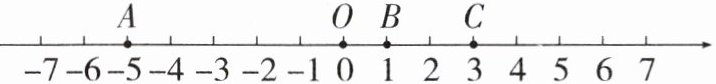
建在C居民區(qū)（3km處），最低成本12000元。

答案：(1) $|x + 5| = 6$表示數(shù)軸上點(diǎn)$x$與$-5$的距離為$6$，則$x + 5 = 6$或$x + 5=-6$，解得$x = 1$或$x=-11$。
(2) $|x + 3| + |x - 1|$表示點(diǎn)$x$到$-3$和$1$的距離之和，當(dāng)$-3\leqslant x\leqslant1$時(shí)，距離之和最小，此時(shí)$x$可取整數(shù)$-3,-2,-1,0,1$；$|x + 3| - |x - 1|$，當(dāng)$x\geqslant1$時(shí)，原式$=(x + 3)-(x - 1)=4$，為最大值。
(3) $|x + 2| + |x + 6| + |x - 1|$表示點(diǎn)$x$到$-6,-2,1$的距離之和，當(dāng)$x=-2$時(shí)，距離之和最小，最小值為$|-2 + 6| + |-2 - 1|=4 + 3=7$。
(4) 設(shè)驛站在數(shù)軸上表示的數(shù)為$x$，總成本$y=1000|x + 5| + 2000|x - 1| + 3000|x - 3|$（單位：元）。當(dāng)$x = 3$時(shí)，$y=1000×8 + 2000×2 + 3000×0=8000 + 4000=12000$元，此時(shí)成本最低。
(1) $1$或$-11$
(2) $-3,-2,-1,0,1$；$4$
(3) $-2$；$7$
(4) 建在$C$居民區(qū)（$3km$處），最低成本$12000$元。
上一頁 下一頁