1. 如圖,在一張透明的紙上畫一條直線l,在l外任取一點(diǎn)Q并折出過(guò)點(diǎn)Q且與l垂直的直線.這樣的直線能折出(
B
)
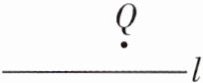
A.0條
B.1條
C.2條
D.3條
答案:B
解析:
根據(jù)垂線的性質(zhì):過(guò)直線外一點(diǎn)有且只有一條直線與已知直線垂直��。
在本題中�,直線$l$外有一點(diǎn)$Q$�����,所以過(guò)點(diǎn)$Q$且與$l$垂直的直線只能折出$1$條���。
答案:B
2. (2024·宿遷期末)如圖,$∠1 = 25^{\circ}$,$∠AOB = 90^{\circ}$,點(diǎn)C,O,D在同一條直線上,則$∠2$的度數(shù)為(
A
)
A.$115^{\circ}$
B.$120^{\circ}$
C.$125^{\circ}$
D.$105^{\circ}$
答案:A
解析:
解:∵∠AOB=90°�����,∠1=25°����,
∴∠COB=∠AOB - ∠1=90° - 25°=65°�����。
∵點(diǎn)C,O�,D在同一條直線上,
∴∠COD=180°��。
∵∠2 + ∠COB=∠COD�,
∴∠2=∠COD - ∠COB=180° - 65°=115°���。
答案:A
3. 如圖,C是線段AB的中點(diǎn),D是線段AC的中點(diǎn),則下列判斷中,錯(cuò)誤的是(
D
)

A.$CD = \frac{1}{4}AB$
B.$CD = AB - BD$
C.$AB = BC + 2CD$
D.$BD = 2CD$
答案:D
解析:
設(shè) $ AB = 4x $��。
∵ $ C $ 是 $ AB $ 中點(diǎn)�,∴ $ AC = BC = \frac{1}{2}AB = 2x $�。
∵ $ D $ 是 $ AC $ 中點(diǎn),∴ $ AD = CD = \frac{1}{2}AC = x $��。
A. $ CD = x = \frac{1}{4}AB $����,正確。
B. $ AB - BD = 4x - (BC + CD) = 4x - (2x + x) = x = CD $�,正確。
C. $ BC + 2CD = 2x + 2x = 4x = AB $���,正確����。
D. $ BD = BC + CD = 2x + x = 3x $,$ 2CD = 2x $�����,$ BD \neq 2CD $���,錯(cuò)誤���。
答案:D
4. (2023·蘇州中考)如圖,在正方形網(wǎng)格內(nèi),線段PQ的兩個(gè)端點(diǎn)都在格點(diǎn)上,網(wǎng)格內(nèi)另有A,B,C,D四個(gè)格點(diǎn),下面四個(gè)結(jié)論中,正確的是(
B
)

A.連接AB,則$AB // PQ$
B.連接BC,則$BC // PQ$
C.連接BD,則$BD \perp PQ$
D.連接AD,則$AD \perp PQ$
答案:B
解析:
設(shè)每個(gè)小正方形邊長(zhǎng)為1,建立平面直角坐標(biāo)系��,設(shè)Q為原點(diǎn)(0,0)��,則P(3,2)��。
PQ的斜率:$k_{PQ}=\frac{2-0}{3-0}=\frac{2}{3}$���。
A. A點(diǎn)坐標(biāo)(3,1)�����,B點(diǎn)坐標(biāo)(2,2)��。
$k_{AB}=\frac{2-1}{2-3}=-1\neq\frac{2}{3}$��,AB不平行PQ��。
B. B點(diǎn)坐標(biāo)(2,2)��,C點(diǎn)坐標(biāo)(-1,0)�。
$k_{BC}=\frac{0-2}{-1-2}=\frac{-2}{-3}=\frac{2}{3}=k_{PQ}$,BC平行PQ���。
C. B點(diǎn)坐標(biāo)(2,2),D點(diǎn)坐標(biāo)(4,-1)����。
$k_{BD}=\frac{-1-2}{4-2}=-\frac{3}{2}$,$k_{PQ}\cdot k_{BD}=\frac{2}{3}×(-\frac{3}{2})=-1$����,BD⊥PQ,但選項(xiàng)B已正確�,繼續(xù)驗(yàn)證D。
D. A點(diǎn)坐標(biāo)(3,1),D點(diǎn)坐標(biāo)(4,-1)�。
$k_{AD}=\frac{-1-1}{4-3}=-2$,$k_{PQ}\cdot k_{AD}=\frac{2}{3}×(-2)=-\frac{4}{3}\neq-1$�����,AD不垂直PQ����。
結(jié)論:正確的是B。
答案:B
5. 如圖,已知四邊形ABCD中,$AB // DC$,連接BD,BE平分$∠ABD$,$BE \perp AD$,$∠EBC和∠DCB$的平分線相交于點(diǎn)F,若$∠ADC = 110^{\circ}$,則$∠F$的度數(shù)為(
D
)
A.$115^{\circ}$
B.$110^{\circ}$
C.$105^{\circ}$
D.$100^{\circ}$
答案:D 解析:因?yàn)?$ BE \perp AD $,所以 $ \angle BED = 90^{\circ} $.又因?yàn)?$ \angle ADC = 110^{\circ} $,所以在四邊形 $ BCDE $ 中, $ \angle BCD + \angle CBE = 360^{\circ} - 90^{\circ} - 110^{\circ} = 160^{\circ} $.因?yàn)?$ \angle EBC $ 和 $ \angle DCB $ 的平分線相交于點(diǎn) $ F $,所以 $ \angle CBF + \angle BCF = \frac{1}{2} \angle EBC + \frac{1}{2} \angle DCB = \frac{1}{2} ( \angle EBC + \angle DCB ) = \frac{1}{2} × 160^{\circ} = 80^{\circ} $,所以在 $ \triangle BCF $ 中, $ \angle F = 180^{\circ} - 80^{\circ} = 100^{\circ} $.故選 D.
6. 如圖,數(shù)軸上M,N,P,Q四點(diǎn)對(duì)應(yīng)的數(shù)都是整數(shù),且點(diǎn)M為線段NQ的中點(diǎn),點(diǎn)P為線段NM的中點(diǎn).若點(diǎn)M對(duì)應(yīng)的整數(shù)是a,點(diǎn)N對(duì)應(yīng)的整數(shù)是b,且$b - 2a = 0$,則數(shù)軸上的原點(diǎn)是(
D
)
A.M
B.N
C.P
D.Q
答案:D 解析:由 $ b - 2a = 0 $ 可得 $ b = 2a $,即點(diǎn) $ N $ 到原點(diǎn)的距離是點(diǎn) $ M $ 到原點(diǎn)距離的兩倍.又因?yàn)辄c(diǎn) $ M $ 為線段 $ NQ $ 的中點(diǎn),所以原點(diǎn)是 $ Q $.故選 D.
7. 若$∠α與∠β$是對(duì)頂角,$∠α的補(bǔ)角是35^{\circ}$,則$∠β$的度數(shù)為
$145^{\circ}$
.
答案:$ 145^{\circ} $
解析:
解:因?yàn)椤夕恋难a(bǔ)角是35°���,所以∠α=180°-35°=145°���。
又因?yàn)椤夕僚c∠β是對(duì)頂角,所以∠β=∠α=145°�����。
145°
8. (2024·泰州校級(jí)月考)從十邊形的一個(gè)頂點(diǎn)畫這個(gè)多邊形的對(duì)角線,最多可畫
7
條.
答案:7
解析:
從n邊形的一個(gè)頂點(diǎn)出發(fā)可以引(n-3)條對(duì)角線���。
對(duì)于十邊形�,n=10�����,所以從一個(gè)頂點(diǎn)出發(fā)可畫對(duì)角線的條數(shù)為:10-3=7(條)
7
9. 如圖所示,添加一個(gè)條件,使$AB // CE$,則添加的條件為
$ \angle B = \angle DCE $ (答案不唯一)
.
答案:$ \angle B = \angle DCE $ (答案不唯一)
解析:
解:添加的條件為$∠B = ∠DCE$(答案不唯一)
10. 如圖,點(diǎn)B與點(diǎn)D在線段AC上,且$BD = \frac{1}{3}AB = \frac{1}{4}CD$,點(diǎn)E,F分別是AB,CD的中點(diǎn),若$CD = 32$,則$EF = $
20
.
答案:20
解析:
解:
∵ $ BD = \frac{1}{4}CD $,$ CD = 32 $�,
∴ $ BD = \frac{1}{4} × 32 = 8 $。
∵ $ BD = \frac{1}{3}AB $�����,
∴ $ AB = 3BD = 3 × 8 = 24 $��。
∵ E 是 AB 中點(diǎn)�,
∴ $ AE = \frac{1}{2}AB = \frac{1}{2} × 24 = 12 $。
∵ F 是 CD 中點(diǎn)��,
∴ $ CF = \frac{1}{2}CD = \frac{1}{2} × 32 = 16 $��。
由圖可知:$ AC = AB + BC = AB + (CD - BD) = 24 + (32 - 8) = 48 $�����。
$ EF = AC - AE - CF = 48 - 12 - 16 = 20 $�����。
20