8. (2024·松原期末)工人師傅需要把一截材料加工成U形零件.如圖,工人師傅先把材料彎成了一個$40^{\circ }$的銳角,然后準(zhǔn)備沿BA在點(diǎn)A處進(jìn)行第二次加工,要保證彎過來的部分與BC平行,則第二次加工需要彎成____°的角.
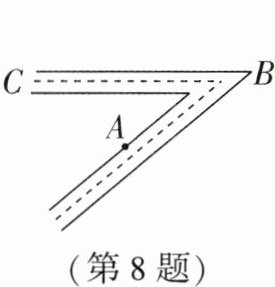
答案:140 解析:根據(jù)題意畫出示意圖如圖,
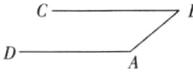
已知∠B = 40°,當(dāng)∠A = 180° - 40° = 140°時,因?yàn)椤螦 + ∠B = 180°,所以AD//BC,所以第二次加工需要彎成140°的角.
9. 將一副三角尺按如圖所示放置,則下列結(jié)論:①$∠1= ∠3$;②若$∠2= 30^{\circ }$,則有$AC// DE$;③若$∠2= 45^{\circ }$,則有$BC// AD$;④若$∠4= ∠C$,必有$∠2= 30^{\circ }$.其中正確的是____
①②③④
(填序號).
答案:①②③④ 解析:因?yàn)椤? + ∠2 = ∠3 + ∠2 = 90°,所以∠1 = ∠3,故①正確.因?yàn)椤? = 30°,所以∠1 = 90° - ∠2 = 60°.又∠E = 60°,所以∠1 = ∠E,所以AC//DE,故②正確.因?yàn)椤? = 45°,所以∠3 = 45°.因?yàn)椤螧 = 45°,所以∠3 = ∠B,所以BC//AD,故③正確.因?yàn)椤? = ∠C = 45°,所以∠CFE = ∠C = 45°.因?yàn)椤螩FE + ∠E = ∠C + ∠1,所以∠1 = ∠E = 60°,所以∠2 = 90° - ∠1 = 30°,故④正確.則其中正確的是①②③④.
解析:
解:①②③④
解析:
①因?yàn)椤?+∠2=90°���,∠3+∠2=90°,所以∠1=∠3�����,故①正確�;
②若∠2=30°����,則∠1=90°-∠2=60°��,又∠E=60°����,所以∠1=∠E�,所以AC//DE,故②正確�;
③若∠2=45°,則∠3=90°-∠2=45°���,又∠B=45°�����,所以∠3=∠B���,所以BC//AD,故③正確����;
④若∠4=∠C=45°����,則∠CFE=∠4=45°�,因?yàn)椤螩FE+∠E=∠C+∠1,∠E=60°����,所以45°+60°=45°+∠1,解得∠1=60°�����,所以∠2=90°-∠1=30°��,故④正確�。
綜上,正確的是①②③④���。
10. 如圖,直線AB和CD被直線MN所截,分別交AB,CD于點(diǎn)E,F.
(1)如圖①,EG平分$∠BEF$,FH平分$∠DFE$(平分的是一對同旁內(nèi)角),則$∠1與∠2$滿足
∠1 + ∠2 = 90°
時,$AB// CD$.
(2)如圖②,EG平分$∠MEB$,FH平分$∠DFE$(平分的是一對同位角),則$∠1與∠2$滿足
∠1 = ∠2
時,$AB// CD$.
(3)如圖③,EG平分$∠AEF$,FH平分$∠DFE$(平分的是一對內(nèi)錯角),則$∠1與∠2$滿足什么條件時,$AB// CD$? 為什么?
∠1 = ∠2.理由:因?yàn)镋G平分∠AEF,FH平分∠DFE,所以∠AEF = 2∠1,∠DFE = 2∠2.因?yàn)椤? = ∠2,所以∠AEF = ∠DFE,所以AB//CD.
答案:(1)∠1 + ∠2 = 90° 解析:因?yàn)镋G平分∠BEF,FH平分∠DFE,所以∠BEF = 2∠1,∠DFE = 2∠2.因?yàn)椤? + ∠2 = 90°,所以∠BEF + ∠DFE = 180°,所以AB//CD.(2)∠1 = ∠2 解析:因?yàn)镋G平分∠BEM,FH平分∠DFE,所以∠BEM = 2∠1,∠DFE = 2∠2.因?yàn)椤? = ∠2,所以∠BEM = ∠DFE,所以AB//CD.(3)∠1 = ∠2.理由:因?yàn)镋G平分∠AEF,FH平分∠DFE,所以∠AEF = 2∠1,∠DFE = 2∠2.因?yàn)椤? = ∠2,所以∠AEF = ∠DFE,所以AB//CD.
解析:
(1)∠1 + ∠2 = 90°
(2)∠1 = ∠2
(3)∠1 = ∠2.
理由:因?yàn)镋G平分∠AEF��,F(xiàn)H平分∠DFE��,
所以∠AEF = 2∠1�����,∠DFE = 2∠2.
因?yàn)椤? = ∠2��,
所以∠AEF = ∠DFE����,
所以AB//CD.
11. 一次數(shù)學(xué)活動中,檢驗(yàn)兩條紙帶①②的邊線是否平行,小明和小麗采用兩種不同的方法:如圖,小明將紙帶①沿AB折疊,量得$∠1= ∠2= 50^{\circ }$;小麗將紙帶②沿GH折疊,發(fā)現(xiàn)直線GD與直線GC重合,直線HF與直線HE重合,則下列判斷正確的是 ( )

A.紙帶①的邊線平行,紙帶②的邊線不平行
B.紙帶①的邊線不平行,紙帶②的邊線平行
C.紙帶①②的邊線都平行
D.紙帶①②的邊線都不平行
答案:B 解析:如紙帶①所示,因?yàn)椤? = ∠2 = 50°,∠1 = ∠3,所以∠3 = ∠2 = 50°.要使得紙帶①的兩邊線平行,則應(yīng)滿足∠4 = ∠2 = 50°,且∠6 = ∠1 = 50°,由折疊可知此時∠5 = ∠4 = 50°.因?yàn)?0° + 50° + 50° = 150°,不能組成平角,所以紙帶①的邊線不可能平行.

如紙帶②所示,因?yàn)镚D與GC重合,HF與HE重合,所以∠CGH = ∠DGH = 90°,∠EHG = ∠FHG = 90°,所以∠CGH + ∠EHG = 180°,所以紙帶②的邊線平行.故選B.
12. 將一副三角尺中的兩個直角頂點(diǎn)C疊放在一起(如圖①),其中$∠A= 30^{\circ },∠B= 60^{\circ },∠D= ∠E= 45^{\circ }$.
(1)猜想$∠BCD與∠ACE$的數(shù)量關(guān)系,并說明理由;
(2)若按住三角尺ABC不動,繞頂點(diǎn)C轉(zhuǎn)動三角尺DCE,試探究$∠BCD$等于多少度時,$CD// AB$,并簡要說明理由;
(3)若$∠BCD= 3∠ACE$,求$∠BCD$的度數(shù),并直接寫出此時DE與AC的位置關(guān)系.

答案:(1)∠BCD + ∠ACE = 180°.理由:因?yàn)椤螧CD = ∠ACB + ∠ACD = 90° + ∠ACD,所以∠BCD + ∠ACE = 90° + ∠ACD + ∠ACE = 90° + 90° = 180°.
(2)當(dāng)∠BCD = 120°或60°時,CD//AB.分兩種情況討論:如圖①,根據(jù)同旁內(nèi)角互補(bǔ),兩直線平行,當(dāng)∠B + ∠BCD = 180°時,CD//AB,此時∠BCD = 180° - ∠B = 180° - 60° = 120°;
如圖②,根據(jù)內(nèi)錯角相等,兩直線平行,當(dāng)∠B = ∠BCD = 60°時,CD//AB.


(3)設(shè)∠ACE = α,則∠BCD = 3α,由(1)可得∠BCD + ∠ACE = 180°,所以3α + α = 180°,所以α = 45°,所以∠BCD = 3α = 135°.此時DE⊥AC或DE//AC.