1. 下列說法中錯誤的個數(shù)為 (
C
)
①過一點有且只有一條直線與已知直線垂直;
②同一平面內(nèi),互相垂直的兩條直線一定相交;
③有公共頂點且相等的角是對頂角.
A.0
B.1
C.2
D.3
答案:C
解析:
①過一點有且只有一條直線與已知直線垂直,需強調(diào)“在同一平面內(nèi)”,原說法錯誤�����;
②同一平面內(nèi),互相垂直的兩條直線一定相交����,正確;
③有公共頂點且相等的角不一定是對頂角����,對頂角還需兩邊互為反向延長線,原說法錯誤�。
錯誤的個數(shù)為2個��。
C
2. (廈門中考)已知直線AB,CB,l在同一平面內(nèi),若$AB⊥l$,垂足為B,$CB⊥l$,垂足也為B,則符合題意的圖形是 (
C
)
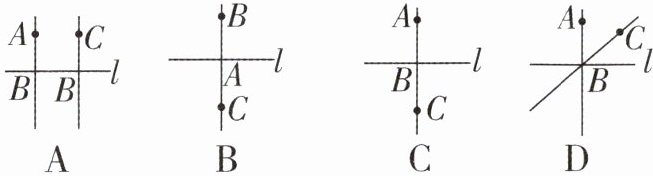
答案:C
解析:
解:根據(jù)題意�����,直線AB���、CB均垂直于直線l�����,且垂足均為點B�����。因此�����,點B是AB�����、CB與l的共同垂足����,AB和CB都經(jīng)過點B并垂直于l。觀察各選項�����,只有選項C中�,AB和CB都以B為垂足垂直于l。
答案:C
3. 教材P175練習T2變式(孝感中考)如圖,直線AB,CD相交于點O,$OE⊥CD$,垂足為點O.若$∠BOE= 40^{\circ }$,則$∠AOC$的度數(shù)為 (
B
)
A.$40^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$140^{\circ }$
答案:B
解析:
解:∵OE⊥CD
∴∠EOD=90°
∵∠BOE=40°
∴∠BOD=∠EOD - ∠BOE=90° - 40°=50°
∵∠AOC與∠BOD是對頂角
∴∠AOC=∠BOD=50°
答案:B
4. 如圖,當$∠1與∠2$滿足
∠1 + ∠2 = 90°
時,$AC⊥BC$.
答案:∠1 + ∠2 = 90°
5. 如圖,OA表示南偏西$20^{\circ }$方向的一條射線,$OA⊥OB$,那么OB的方向可表示為
南偏東70°
.
答案:南偏東70°
解析:
解:因為OA表示南偏西$20^{\circ}$方向,所以OA與正南方向的夾角為$20^{\circ}$����。
由于$OA⊥OB$,則OA與OB的夾角為$90^{\circ}$����。
所以OB與正南方向的夾角為$90^{\circ}-20^{\circ}=70^{\circ}$,且OB在正南方向的東側(cè)����。
因此,OB的方向可表示為南偏東$70^{\circ}$���。
南偏東$70^{\circ}$
6. 如圖,在方格紙中,點C在直線AB外.
(1)請過點C畫直線AB的垂線CD;
(2)過點C畫CD的垂線CH;
(3)通過你的觀察,直線CH和直線AB是否會相交:____.(填“是”或“否”)

答案:(1)(2)如圖所示

(3)否
7. 如圖,直線AB,CD相交于點O,射線OE,OF分別平分$∠AOD,∠BOD,∠AOC= 26^{\circ }$.
(1)求$∠BOF$的度數(shù);
(2)判斷射線OE,OF之間有怎樣的位置關系,并說明理由.

答案:(1)因為直線AB�,CD相交于點O�����,∠AOC = 26°����,所以∠BOD = ∠AOC = 26°����。因為OF平分∠BOD�����,所以∠BOF = $\frac{1}{2}$∠BOD = $\frac{1}{2}$×26° = 13°���。
(2) OE⊥OF。理由:因為OE平分∠AOD���,OF平分∠BOD��,所以∠DOE = $\frac{1}{2}$∠AOD��,∠DOF = $\frac{1}{2}$∠BOD����,所以∠DOE + ∠DOF = $\frac{1}{2}$(∠AOD + ∠BOD) = $\frac{1}{2}$×180° = 90°���,即∠EOF = 90°�,所以OE⊥OF�����。
8. 新趨勢 跨學科融合(2025·上海期中)如圖,小軒的乒乓球掉到沙發(fā)下,他借助平面鏡反射的原理找到了乒乓球的位置.已知法線$OC⊥MN$,反射光線OA與水平線的夾角$∠AOD= 56^{\circ }$,則平面鏡MN與水平線BD的夾角$∠BOM$的大小為(入射光線與鏡面的夾角等于反射光線與鏡面的夾角) (
B
)
A.$24^{\circ }$
B.$28^{\circ }$
C.$34^{\circ }$
D.$56^{\circ }$
答案:B 解析:因為∠AOD = 56°,所以∠AOB = 180° - ∠AOD = 124°����。因為入射光線與鏡面的夾角等于反射光線與鏡面的夾角,所以∠AOC = ∠BOC = $\frac{1}{2}$∠AOB = $\frac{1}{2}$×124° = 62°�。因為OC⊥MN,所以∠COM = 90°�����,所以∠BOM = ∠COM - ∠BOC = 90° - 62° = 28°��,故選B�。