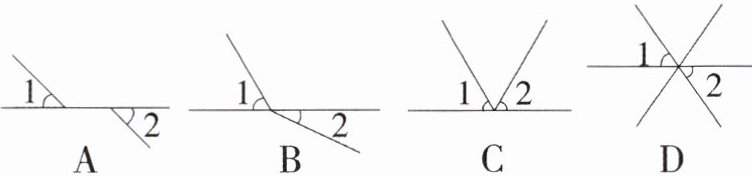
1. 教材P172練習T1變式 (2024·北京期中)下列各圖中,$∠1和∠2$是對頂角的是 (
D
)
答案:D
解析:
根據(jù)對頂角的定義:兩條直線相交后所得的只有一個公共頂點且兩邊互為反向延長線的兩個角叫做對頂角。
分析各選項:
選項A:∠1和∠2沒有公共頂點�����,不是對頂角�。
選項B:∠1和∠2的兩邊不互為反向延長線,不是對頂角����。
選項C:∠1和∠2的兩邊不互為反向延長線,不是對頂角����。
選項D:∠1和∠2有公共頂點,且兩邊互為反向延長線�,是對頂角。
答案:D
2. 下列說法中正確的是 (
D
)
A.相等的角是對頂角
B.兩條直線相交所成的兩個角是對頂角
C.有公共頂點,并且相等的角是對頂角
D.對頂角的余角和補角都相等
答案:D
解析:
解:A. 相等的角不一定是對頂角�����,例如兩直線平行時同位角相等,但同位角不是對頂角�,故A錯誤;
B. 兩條直線相交所成的鄰補角不是對頂角����,故B錯誤;
C. 有公共頂點且相等的角不一定是對頂角��,例如角平分線分成的兩個角���,故C錯誤�;
D. 對頂角相等�,所以它們的余角和補角都相等,故D正確�。
答案:D
3. 新趨勢 跨學科融合 (2025·吉安模擬)光線從空氣斜射向水中時會發(fā)生折射現(xiàn)象,如圖,長

方形ABFE為盛滿水的水槽,一束光線從點P射向水面上的點D,折射后照到水槽底部的點C.測得$α=40^{\circ },β=30^{\circ }$,若P,D,B三點在同一條直線上,則$∠BDC$的度數(shù)為 (
D
)
A.$40^{\circ }$
B.$30^{\circ }$
C.$20^{\circ }$
D.$10^{\circ }$
答案:D
解析:
解:由題意知,光線從空氣斜射向水中��,∠α=40°為入射角�����,∠β=30°為折射角�����。
因為ABFE是長方形,所以水面EF與底部AB平行�,過點D作水面EF的垂線(法線),則法線與EF垂直�����。
入射角α為入射光線PD與法線的夾角�����,折射角β為折射光線DC與法線的夾角��。
由于P����、D��、B三點共線����,直線PDB與法線的夾角為α=40°,折射光線DC與法線的夾角為β=30°��,
所以∠BDC=α - β=40° - 30°=10°�����。
答案:D
4. 如圖,直線a,b相交于點O,將量角器的中心與點O重合,發(fā)現(xiàn)表示$60^{\circ }$的點在直線a上,表示$135^{\circ }$的點在直線b上,則$∠1= $
75
$^{\circ }$.

答案:75
解析:
解:由量角器讀數(shù)可知,直線a對應的刻度為$60^{\circ}$��,直線b對應的刻度為$135^{\circ}$�。
兩刻度差為$135^{\circ}-60^{\circ}=75^{\circ}$,即直線a與直線b的夾角為$75^{\circ}$����。
因為$\angle1$是直線a與直線b相交形成的角,所以$\angle1 = 75^{\circ}$�。
75
5. (1)如圖①,直線AB,CD,EF相交于點O,$∠1= 20^{\circ },∠BOC= 80^{\circ }$,則$∠2$的度數(shù)為
$60^\circ$
.
(2)如圖②,已知直線AB和CD相交于點O,$∠COE$是直角,OF平分$∠AOE,∠COF= 24^{\circ }$,則$∠BOD$的度數(shù)為
42
$^{\circ }$.

答案:(1) $60^\circ$ (2) 42
解析:
(1)
∵∠BOC=80°,∠1=20°����,
∴∠BOF=∠BOC - ∠1=80° - 20°=60°,
∵∠2與∠BOF是對頂角���,
∴∠2=∠BOF=60°����。
(2)
∵∠COE是直角��,
∴∠COE=90°,
∵∠COF=24°�,
∴∠EOF=∠COE - ∠COF=90° - 24°=66°,
∵OF平分∠AOE��,
∴∠AOE=2∠EOF=2×66°=132°���,
∵∠AOC=∠AOE - ∠COE=132° - 90°=42°���,
∵∠BOD與∠AOC是對頂角����,
∴∠BOD=∠AOC=42°。
答案:(1)60°����;(2)42。
6. 如圖,直線AB,CD相交于點O,OE平分$∠AOD,∠FOC= 90^{\circ },∠1= 40^{\circ }$,求$∠2和∠3$的度數(shù).

答案:因為 $ \angle FOC = 90^\circ $�����,$ \angle 1 = 40^\circ $����,AB 為直線,所以 $ \angle 3 + \angle FOC + \angle 1 = 180^\circ $,所以 $ \angle 3 = 180^\circ - 90^\circ - 40^\circ = 50^\circ $����。因為 $ \angle AOD $ 和 $ \angle BOC $ 為對頂角,所以 $ \angle AOD = 40^\circ + 90^\circ = 130^\circ $�����。因為 OE 平分 $ \angle AOD $�����,所以 $ \angle 2 = \frac{1}{2} \angle AOD = 65^\circ $�����。
解析:
解:因為 $ \angle FOC = 90^\circ $��,$ \angle 1 = 40^\circ $����,AB為直線,
所以 $ \angle 3 + \angle FOC + \angle 1 = 180^\circ $�,
所以 $ \angle 3 = 180^\circ - \angle FOC - \angle 1 = 180^\circ - 90^\circ - 40^\circ = 50^\circ $。
因為 $ \angle AOD $ 與 $ \angle BOC $ 是對頂角��,
且 $ \angle BOC = \angle 1 + \angle FOC = 40^\circ + 90^\circ = 130^\circ $,
所以 $ \angle AOD = \angle BOC = 130^\circ $�����。
因為 OE 平分 $ \angle AOD $���,
所以 $ \angle 2 = \frac{1}{2} \angle AOD = \frac{1}{2} × 130^\circ = 65^\circ $����。
綜上����,$ \angle 2 = 65^\circ $��,$ \angle 3 = 50^\circ $�。
7. (2024·高密月考)如圖,直線AB與CD相交于點O,$∠DOE= α,∠DOF:∠AOD= 2:3$,射線OE平分$∠BOF$,則$∠BOC= $ (
D
)
A.$30^{\circ }$
B.$40^{\circ }$
C.$540^{\circ }-5α$
D.$540^{\circ }-6α$
答案:D 解析:設 $ \angle DOF = 2x $,則 $ \angle AOD = 3x $�����,所以 $ \angle AOF = 5x $�����,所以 $ \angle BOF = 180^\circ - 5x $。因為 OE 平分 $ \angle BOF $��,所以 $ \angle FOE = \frac{1}{2} \angle BOF = \frac{1}{2}(180^\circ - 5x) = 90^\circ - \frac{5}{2}x $���。因為 $ \angle DOE = \alpha $��,所以 $ \angle DOF + \angle FOE = \alpha $���,即 $ 2x + 90^\circ - \frac{5}{2}x = \alpha $,解得 $ x = 180^\circ - 2\alpha $�����。則 $ \angle AOD = 3x = 3 × (180^\circ - 2\alpha) = 540^\circ - 6\alpha $��,所以 $ \angle BOC = \angle AOD = 540^\circ - 6\alpha $����。故選 D。
8. (2024·深圳期中)如圖,直線AB,CD相交于點O,$∠AOE= 90^{\circ },∠DOF= 90^{\circ }$,OB平分$∠DOG$,給出下列結論:①當$∠AOF= 60^{\circ }$時,$∠DOE= 60^{\circ }$;②與$∠BOD$相等的角有三個;③OD為$∠EOG$的平分線;④$∠COG= 180^{\circ }-2∠EOF$.其中正確的結論有 (
C
)

A.1個
B.2個
C.3個
D.4個
答案:C 解析:$ \angle AOF + \angle EOF = \angle DOE + \angle EOF = 90^\circ $�,因此 $ \angle AOF = \angle DOE $,當 $ \angle AOF = 60^\circ $ 時��,$ \angle DOE = 60^\circ $��,正確,故 ① 符合題意��;OB 平分 $ \angle GOD $�,因此 $ \angle GOD = 2 \angle BOD $,而 $ \angle DOE = 90^\circ - \angle BOD $�,所以 $ \angle DOE $ 不一定等于 $ \angle GOD $,因此 OD 不一定是 $ \angle EOG $ 的平分線����,故 ③ 不符合題意;$ \angle EOF + \angle EOD = \angle BOD + \angle EOD = 90^\circ $��,因此 $ \angle EOF = \angle BOD $��,由 OB 平分 $ \angle GOD $ 得到 $ \angle GOB = \angle BOD $�,又 $ \angle AOC = \angle BOD $,因此與 $ \angle BOD $ 相等的角有三個�,正確�,故 ② 符合題意;$ \angle COG = \angle AOB - \angle AOC - \angle GOB = \angle AOB - 2 \angle EOF = 180^\circ - 2 \angle EOF $�,正確,故 ④ 符合題意��。其中正確的結論有 3 個���。故選 C��。