1. (2024·泰州校級模擬)已知$∠α=42^{\circ }12'$,與$∠α$互余的角的度數(shù)是 (
D
)
A.$132^{\circ }12'$
B.$137^{\circ }48'$
C.$57^{\circ }48'$
D.$47^{\circ }48'$
答案:D
解析:
解:因?yàn)榛ビ嗟膬蓚€角的和為$90^{\circ}$��,$∠α = 42^{\circ}12'$�,所以與$∠α$互余的角的度數(shù)是$90^{\circ}-42^{\circ}12' = 47^{\circ}48'$��。
答案:D
2. (通遼中考)如圖,將一副三角尺按下列位置擺放,使$∠α和∠β$互余的擺放方式是(
A
)
答案:A
解析:
解:A選項(xiàng)中����,一副三角尺的直角頂點(diǎn)重合,∠α與∠β和直角構(gòu)成一個平角�,即∠α + ∠β + 90° = 180°,所以∠α + ∠β = 90°�,∠α和∠β互余。
B��、C�����、D選項(xiàng)中∠α和∠β的和均不等于90°���。
結(jié)論:A
3. 下列四種說法:①銳角的補(bǔ)角一定是鈍角;②一個角的補(bǔ)角一定大于這個角;③如果兩個角是同一個角的補(bǔ)角,那么它們相等;④一個銳角的余角一定小于這個角的補(bǔ)角.其中正確的有 (
C
)
A.1個
B.2個
C.3個
D.4個
答案:C
解析:
①設(shè)銳角為α(0°<α<90°)�,則其補(bǔ)角為180°-α���,90°<180°-α<180°���,是鈍角���,正確;
②直角的補(bǔ)角是直角���,等于這個角����,鈍角的補(bǔ)角是銳角����,小于這個角�����,錯誤��;
③同角的補(bǔ)角相等����,正確����;
④銳角α的余角為90°-α��,補(bǔ)角為180°-α���,90°-α<180°-α�,正確�����。
正確的有①③④�,共3個。
答案:C
4. (1)已知$∠A的補(bǔ)角為120^{\circ }$,則$∠A$的余角為
30
$^{\circ }$.
(2)已知$∠1與∠2$互余,且$∠1= 35^{\circ }$,則$∠2$的補(bǔ)角為
125
$^{\circ }$.
答案:(1)30 (2)125
解析:
(1)解:因?yàn)椤螦的補(bǔ)角為120°��,所以∠A=180°-120°=60°����,則∠A的余角為90°-60°=30°。
(2)解:因?yàn)椤?與∠2互余�����,∠1=35°,所以∠2=90°-35°=55°�,則∠2的補(bǔ)角為180°-55°=125°。
5. (1)(自貢中考改編)如果一個角的度數(shù)比它補(bǔ)角的2倍多$30^{\circ }$,求這個角的度數(shù).
(2)一個角的補(bǔ)角加上$10^{\circ }$后,等于這個角的余角的3倍,求這個角以及它的余角和補(bǔ)角的度數(shù).
答案:(1)設(shè)這個角是$x^{\circ}$�。根據(jù)題意,得$x = 2(180 - x)+30$����,解得$x = 130$,即這個角的度數(shù)為$130^{\circ}$����。
(2)設(shè)這個角為$x^{\circ}$。根據(jù)題意�,得$180 - x + 10 = 3(90 - x)$,解得$x = 40$�,即這個角是$40^{\circ}$,它的余角是$50^{\circ}$����,補(bǔ)角是$140^{\circ}$�����。
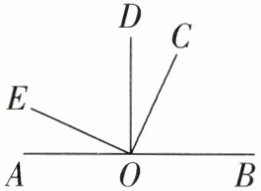
6. 如圖,$AB$是一條直線,$∠AOD= ∠BOD= ∠EOC= 90^{\circ },∠BOC:∠AOE= 3:1$.
(1)求$∠COD$的度數(shù).
(2)圖中有哪幾對角互為余角?
(3)圖中有哪幾對角互為補(bǔ)角?
答案:(1)因?yàn)?∠AOD = ∠BOD = ∠EOC = 90^{\circ}$�,所以$∠BOC + ∠AOE = 90^{\circ}$。因?yàn)?∠BOC:∠AOE = 3:1$,所以$∠BOC=\frac{3}{3 + 1}×90^{\circ}=67.5^{\circ}$���,所以$∠COD = 90^{\circ}-67.5^{\circ}=22.5^{\circ}$���。
(2)互余的角有$∠COB$與$∠COD$,$∠COB$與$∠AOE$����,$∠DOE$與$∠COD$,$∠DOE$與$∠AOE$���。
(3)互補(bǔ)的角有$∠COB$與$∠COA$�,$∠AOE$與$∠EOB$�,$∠AOD$與$∠BOD$,$∠AOD$與$∠EOC$�����,$∠BOD$與$∠EOC$���,$∠EOD$與$∠AOC$��,$∠DOC$與$∠EOB$����。
7. 已知$∠α$是銳角,$∠α與∠β$互補(bǔ),$∠α與∠γ$互余,則$∠β與∠γ$的關(guān)系式為 (
A
)
A.$∠β-∠γ= 90^{\circ }$
B.$∠β+∠γ= 90^{\circ }$
C.$∠β+∠γ= 80^{\circ }$
D.$∠β-∠γ= 180^{\circ }$
答案:A 解析:因?yàn)?∠α$與$∠β$互補(bǔ),$∠α$與$∠γ$互余����,所以$∠α + ∠β = 180^{\circ}$,$∠α + ∠γ = 90^{\circ}$�。所以$∠β - ∠γ = 90^{\circ}$。故選A�。
8. 如圖,$∠AOB= 90^{\circ }$,直線$b經(jīng)過點(diǎn)O$.在下面的五個式子中:①$180^{\circ }-∠2$;②$∠3$;③$2∠1+∠2$;④$2∠3-2∠1-∠2$;⑤$180^{\circ }-∠1$.等于$∠2$的補(bǔ)角的式子的個數(shù)是 (
C
)

A.2
B.3
C.4
D.5
答案:C 解析:因?yàn)?∠AOB = 90^{\circ}$,所以$∠1 + ∠2 = 90^{\circ}$�����。因?yàn)橹本€$b$經(jīng)過點(diǎn)$O$�,所以$∠2 + ∠3 = 180^{\circ}$,$∠3 = 180^{\circ}-∠2$����,故①符合題意;②由①知����,$∠3$是$∠2$的補(bǔ)角,故②符合題意����;因?yàn)?2(∠1 + ∠2)=180^{\circ}$,所以$∠2 = 180^{\circ}-(2∠1 + ∠2)$�����,故③符合題意�����;因?yàn)?∠3 = 180^{\circ}-∠2$��,$∠1 = 90^{\circ}-∠2$�,所以$2∠3 - 2∠1 - ∠2 = 2(180^{\circ}-∠2)-2(90^{\circ}-∠2)-∠2 = 180^{\circ}-∠2$,故④符合題意��;因?yàn)?180^{\circ}-∠1 + ∠2 ≠ 180^{\circ}$���,所以⑤不符合題意�。故選C�。