1. (2025·沂州期末)如圖,C 為 AB 的中點,點 D 在線段 AC 上,且 $ AD:DB = 1:7 $, $ DC = 6 $,則 AB 的長度為 (
A
)
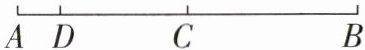
A.16
B.14
C.12
D.10
答案:A
解析:
解:設(shè) $AD = x$�,則 $DB = 7x$。
因為 $AB = AD + DB$��,所以 $AB = x + 7x = 8x$。
又因為 $C$ 為 $AB$ 的中點,所以 $AC = \frac{1}{2}AB = 4x$����。
由于 $DC = AC - AD$�,且 $DC = 6$����,
則 $4x - x = 6$,解得 $x = 2$�。
因此 $AB = 8x = 8×2 = 16$。
答案:A
2. 如圖,在一條數(shù)軸上有若干個點,任意兩個相鄰點間的距離都為 2 個單位長度,其中 A,B,C 三點所對應(yīng)的數(shù)分別為 a,b,c,若 $ 3a + c = 4 $,則 b 的值為______.

$\frac{5}{2}$
答案:$\frac{5}{2}$解析:觀察題圖可知c=a+10,代入3a+c=4,得3a+a+10=4,解得a=$-\frac{3}{2}$,則b=a+4=$\frac{5}{2}$.
解析:
解:由數(shù)軸可知��,A���、B�、C三點相鄰兩點間距離為2�����,且A到B有2段距離�,A到C有5段距離,所以$b = a + 2×2 = a + 4$�����,$c = a + 2×5 = a + 10$。
將$c = a + 10$代入$3a + c = 4$����,得$3a + a + 10 = 4$,
$4a = 4 - 10$�,
$4a = -6$,
解得$a = -\frac{3}{2}$�����。
則$b = -\frac{3}{2} + 4 = \frac{5}{2}$����。
$\frac{5}{2}$
3. 如圖,在數(shù)軸上有 A,B,C,D 四個整數(shù)點(即各點均表示整數(shù)),且 $ 2AB = BC = 3CD $,如果 A,D 兩點表示的數(shù)分別為 -5 和 6,那么該數(shù)軸上點 C 表示的整數(shù)是______.

4
答案:4解析:設(shè)BC=6x,因為2AB=BC=3CD,所以AB=3x,CD=2x,所以AD=AB+BC+CD=11x.因為A,D兩點表示的數(shù)分別是?5和6,所以11x=11,解得x=1,所以AB=3,BC=6,CD=2.因為A,D兩點表示的數(shù)分別為?5和6,所以點C表示的整數(shù)是4.
解析:
設(shè) $ BC = 6x $����,
因為 $ 2AB = BC = 3CD $,所以 $ AB = 3x $����,$ CD = 2x $,
則 $ AD = AB + BC + CD = 3x + 6x + 2x = 11x $�����。
由于 $ A $,$ D $ 兩點表示的數(shù)分別為 $-5$ 和 $6$����,
所以 $ AD = 6 - (-5) = 11 $,即 $ 11x = 11 $����,解得 $ x = 1 $��。
因此 $ CD = 2x = 2 $�����,
點 $ C $ 表示的數(shù)為 $ D $ 點表示的數(shù)減去 $ CD $ 的長度�����,即 $ 6 - 2 = 4 $�。
4
4. 新趨勢 過程性學(xué)習(xí) 如圖,已知線段 $ AB = 10 $,C 是線段 AB 延長線上的一點,點 D 是 AC 的中點.若點 E 為線段 CD 上一點,且 $ DE = 5 $,試說明點 E 是線段 BC 的中點.
小明的做法如下,請你幫他完成解答過程.
解:設(shè) $ BC = x $.
......
......

答案:設(shè)BC=x,AC=AB+BC=10+x,因為點D是AC的中點,所以DC=$\frac{1}{2}$AC=$\frac{1}{2}$(10+x)=5+$\frac{1}{2}$x.因為DE=5,所以EC=DC?DE=5+$\frac{1}{2}$x?5=$\frac{1}{2}$x,所以BE=BC?EC=x?$\frac{1}{2}$x=$\frac{1}{2}$x,所以BE=EC,所以點E是線段BC的中點
5. 如圖,已知 B 是線段 AC 上一點,M 是線段 AB 的中點,N 是線段 AC 的中點,P 為 NA 的中點,Q 為 MA 的中點,求 $ \frac{MN}{PQ} $的值.

答案:解法一:由題意,得PQ=AP?AQ=$\frac{1}{2}$AN?$\frac{1}{2}$AM=$\frac{1}{2}$(AN?AM)=$\frac{1}{2}$MN,所以$\frac{MN}{PQ}$=2. 解法二:設(shè)AC=x,AB=y,則AN=$\frac{1}{2}$x,AM=$\frac{1}{2}$y.因此MN=AN?AM=$\frac{1}{2}$x?$\frac{1}{2}$y=$\frac{1}{2}$(x?y).同理可得PQ=$\frac{1}{2}$MN=$\frac{1}{4}$(x?y),故$\frac{MN}{PQ}$=2.
解析:
解:設(shè) $ AC = x $,$ AB = y $���。
因為 $ N $ 是 $ AC $ 的中點����,所以 $ AN = \frac{1}{2}AC = \frac{1}{2}x $;
因為 $ M $ 是 $ AB $ 的中點��,所以 $ AM = \frac{1}{2}AB = \frac{1}{2}y $����。
則 $ MN = AN - AM = \frac{1}{2}x - \frac{1}{2}y = \frac{1}{2}(x - y) $。
因為 $ P $ 是 $ NA $ 的中點���,所以 $ AP = \frac{1}{2}AN = \frac{1}{2} × \frac{1}{2}x = \frac{1}{4}x $����;
因為 $ Q $ 是 $ MA $ 的中點��,所以 $ AQ = \frac{1}{2}AM = \frac{1}{2} × \frac{1}{2}y = \frac{1}{4}y $�����。
則 $ PQ = AP - AQ = \frac{1}{4}x - \frac{1}{4}y = \frac{1}{4}(x - y) $����。
因此,$ \frac{MN}{PQ} = \frac{\frac{1}{2}(x - y)}{\frac{1}{4}(x - y)} = 2 $�����。
答案:$ 2 $
6. 如圖,點 C,D 是線段 AB 上的任意兩點,點 E 是 AC 的中點,點 F 是 BD 的中點,如果 $ EF = m $, $ CD = n $,那么線段 AB 的長度為 (
C
)
A.$ m + n $
B.$ 2m + n $
C.$ 2m - n $
D.$ 3m - 2n $
答案:C解析:由題意得EC+FD=EF?CD=m?n.因為E是AC的中點,F 是BD的中點,所以AE+FB=EC+FD=EF?CD=m?n.又因為AB=AE+FB+EF,所以AB=m?n+m=2m?n.故選C.
7. 如圖,已知線段 $ AM:BM = \frac{3}{4} $, $ GM:MN = \frac{3}{4} $,且 $ BN = 10 $,則 $ AG = $
$\frac{15}{2}$
.
答案:$\frac{15}{2}$解析:由題意得AM=$\frac{3}{4}$BM,GM=$\frac{3}{4}$MN,則AG=AM?GM=$\frac{3}{4}$BM - $\frac{3}{4}$MN=$\frac{3}{4}$(BM?MN)=$\frac{3}{4}$BN=$\frac{3}{4}$×10=$\frac{15}{2}$.
解析:
解:由題意得,$AM = \frac{3}{4}BM$����,$GM = \frac{3}{4}MN$。
則$AG = AM - GM = \frac{3}{4}BM - \frac{3}{4}MN = \frac{3}{4}(BM - MN)$��。
因為$BM - MN = BN$�����,且$BN = 10$��,
所以$AG = \frac{3}{4}BN = \frac{3}{4}×10 = \frac{15}{2}$��。
$\frac{15}{2}$
8. 如圖,C,D 是線段 AB 上的兩點,已知 $ AB = 10cm $, $ CD = 3cm $,則以 A,C,D,B 這四個點為端點的所有線段的長度之和為
33
cm.
答案:33解析:因為AC+BC=AB,AD+BD=AB,且AB=10cm,CD=3cm,所以所有線段之和為AC+AD+AB+CD+CB+BD=(AC+BC)+(AD+BD)+AB+CD=3AB+CD=3×10+3=33(cm).
解析:
解:以A,C,D,B為端點的線段有AC,AD,AB,CD,CB,DB���。
所有線段長度之和為:AC+AD+AB+CD+CB+DB。
因為AC+CB=AB����,AD+DB=AB,AB=10cm�����,CD=3cm,
所以原式=(AC+CB)+(AD+DB)+AB+CD=AB+AB+AB+CD=3AB+CD���。
則3×10+3=33(cm)���。
答案:33
9. 如圖,C,D 是線段 AB 上兩點,M,N 分別是線段 AD,BC 的中點,下列結(jié)論:
①若 $ AD = BM $,則 $ AB = 3BD $;
②若 $ AC = BD $,則 $ AM = BN $;
③ $ AC - BD = 2(MC - DN) $;
④ $ 2MN = AB - CD $.
其中正確的結(jié)論是______(填序號).

①②③④
答案:①②③④解析:①若AD=BM,則AM=BD.由M是AD的中點,得AM=MD,則AM=MD=BD,故AB=3BD.②若AC=BD,則AD=BC.由M,N分別是AD,BC的中點,可得AM=$\frac{1}{2}$AD,BN=$\frac{1}{2}$BC,故AM=BN.③因為AC=AM+MC=DM+MC,BD=BN+DN=CN+DN,所以AC?BD=DM?CN+MC?DN.又因為DM?CN=MC?DN,故AC?BD=2(MC?DN).④因為MN=MD+CN?CD=$\frac{1}{2}$AD+$\frac{1}{2}$BC?CD=$\frac{1}{2}$(AD+BC)?CD=$\frac{1}{2}$(AB+CD)?CD=$\frac{1}{2}$(AB?CD),故2MN=AB?CD.綜上,其中正確的結(jié)論是①②③④.