1. (2025·信陽期末)已知點(diǎn)B在線段AC上,點(diǎn)D在線段AB上,
(1)如圖①,若AB= 6 cm,BC= 4 cm,D為線段AC的中點(diǎn),求線段DB的長度;
(2)如圖②,若AB= 4BD,CD= 3BD,E為線段AB的中點(diǎn),EC= 12 cm,求線段AC的長度.
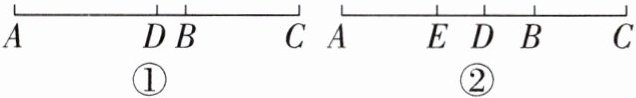
答案:(1)因為 $ AC = AB + BC $�,$ AB = 6 \text{ cm} $,$ BC = 4 \text{ cm} $�,所以 $ AC = AB + BC = 6 + 4 = 10(\text{cm}) $����,又因為 $ D $ 為線段 $ AC $ 的中點(diǎn)���,所以 $ DC = \frac{1}{2}AC = \frac{1}{2} × 10 = 5(\text{cm}) $���,所以 $ DB = DC - BC = 5 - 4 = 1(\text{cm}) $。
(2)設(shè) $ BD = x \text{ cm} $�����,因為 $ AB = 4BD $��,$ CD = 3BD $���,所以 $ AB = 4BD = 4x \text{ cm} $��,$ CD = 3BD = 3x \text{ cm} $��。因為 $ DC = DB + BC $���,所以 $ BC = CD - DB = 3x - x = 2x(\text{cm}) $。因為 $ AC = AB + BC $�����,所以 $ AC = 4x + 2x = 6x(\text{cm}) $����。因為 $ E $ 為線段 $ AB $ 的中點(diǎn)�����,所以 $ BE = \frac{1}{2}AB = \frac{1}{2} × 4x = 2x(\text{cm}) $���。
因為 $ EC = BE + BC $,所以 $ EC = 2x + 2x = 4x(\text{cm}) $��。又因為 $ EC = 12 \text{ cm} $���,所以 $ 4x = 12 $���,解得 $ x = 3 $,所以 $ AC = 6x = 6 × 3 = 18(\text{cm}) $�����。
2. (2025·南陽期末)如圖,線段AB= 28,動點(diǎn)P從點(diǎn)A出發(fā),以每秒2個單位長度的速度向點(diǎn)B運(yùn)動,M為AP的中點(diǎn),N為BP的中點(diǎn).
(1)點(diǎn)P出發(fā)
7
s后,PB= 2AM.
(2)在點(diǎn)P的運(yùn)動過程中,有如下兩個結(jié)論:①M(fèi)N的長度不變;②2BM-BP的長度不變.請選擇一個正確的結(jié)論,并求出其值.

選①�����,MN的長度不變��。理由如下:因為點(diǎn)M為線段AP的中點(diǎn)�,點(diǎn)N為線段BP的中點(diǎn)����,所以MP=1/2AP���,PN=1/2PB,所以MN=MP+PN=1/2AP+1/2PB=1/2(AP+PB)=1/2AB=1/2×28=14��。
答案:(1)7 解析:設(shè)出發(fā) $ x \text{ s} $ 后 $ PB = 2AM $����,$ PA = 2x $,$ PB = 28 - 2x $�����,因為 $ M $ 為 $ AP $ 的中點(diǎn)�,所以 $ AM = x $,由題意得 $ 28 - 2x = 2x $���,解得 $ x = 7 $����。
(2)選①�,$ MN $ 的長度不變���。理由如下:因為點(diǎn) $ M $ 為線段 $ AP $ 的中點(diǎn),點(diǎn) $ N $ 為線段 $ BP $ 的中點(diǎn)���,所以 $ MP = \frac{1}{2}AP $����,$ PN = \frac{1}{2}PB $����,
所以 $ MN = MP + PN = \frac{1}{2}AP + \frac{1}{2}PB = \frac{1}{2}(AP + PB) = \frac{1}{2}AB = \frac{1}{2} × 28 = 14 $。
選②����,$ 2BM - BP $ 的長度不變。理由如下:$ 2BM - BP = BM + (BM - BP) = BM + MP $�����。因為點(diǎn) $ M $ 為線段 $ AP $ 的中點(diǎn)�,所以 $ MP = AM $,所以 $ 2BM - BP = BM + AM = AB = 28 $�。
3. (2025·達(dá)州期末)如圖,點(diǎn)B,C是線段AD上的兩點(diǎn),點(diǎn)M和點(diǎn)N分別在線段AB和線段CD上.
(1)當(dāng)AD= 8,MN= 6,點(diǎn)M,N分別是線段AB,CD的中點(diǎn)時,BC= ______
4
;
(2)若AD= a,MN= b,當(dāng)AM= 2BM,DN= 2CN時,求BC的長度.(用含a和b的代數(shù)式表示)
$\frac{3}{2}b - \frac{1}{2}a$
答案:(1)4 解析:因為 $ AD = 8 $,$ MN = 6 $,所以 $ AM + DN = AD - MN = 8 - 6 = 2 $�����。因為點(diǎn) $ M $�����,$ N $ 分別是線段 $ AB $�����,$ CD $ 的中點(diǎn)�,所以 $ AM = BM $�,$ CN = DN $,所以 $ AB + CD = 2AM + 2DN = 2(AM + DN) = 2 × 2 = 4 $�����,所以 $ BC = AD - (AB + CD) = 8 - 4 = 4 $��。
(2)因為 $ AD = a $��,$ MN = b $��,所以 $ AM + DN = AD - MN = a - b $。因為 $ AM = 2BM $�����,$ DN = 2CN $���,所以 $ AB + CD = \frac{3}{2}(AM + DN) = \frac{3}{2}(a - b) $�����,所以 $ BC = AD - (AB + CD) = a - \frac{3}{2}(a - b) = \frac{3}{2}b - \frac{1}{2}a $���。
4. 如圖,點(diǎn)B,D在線段AC上,且BD= $\frac{1}{3}$AB= $\frac{1}{4}$CD,E,F分別是AB,CD的中點(diǎn),EF= 10 cm,求AB的長度.

答案:由 $ BD = \frac{1}{3}AB = \frac{1}{4}CD $,得 $ AB = 3BD $�����,$ CD = 4BD $���,所以 $ AD = AB - BD = 2BD $�,所以 $ AC = AD + CD = 2BD + 4BD = 6BD $�����。因為 $ E $,$ F $ 分別是 $ AB $����,$ CD $ 的中點(diǎn),所以 $ AE = \frac{1}{2}AB = \frac{3}{2}BD $��,$ FC = \frac{1}{2}CD = 2BD $�����,$ EF = AC - AE - FC = 6BD - \frac{3}{2}BD - 2BD = \frac{5}{2}BD = 10 \text{ cm} $����,解得 $ BD = 4 \text{ cm} $��,則 $ AB = 3BD = 3 × 4 = 12(\text{cm}) $�����。
解析:
解:設(shè) $ BD = x \, \text{cm} $�����,
由 $ BD = \frac{1}{3}AB = \frac{1}{4}CD $����,得 $ AB = 3x \, \text{cm} $�,$ CD = 4x \, \text{cm} $�����。
$ AD = AB - BD = 3x - x = 2x \, \text{cm} $��,
$ AC = AD + CD = 2x + 4x = 6x \, \text{cm} $���。
因為 $ E $��,$ F $ 分別是 $ AB $����,$ CD $ 的中點(diǎn)����,
所以 $ AE = \frac{1}{2}AB = \frac{3}{2}x \, \text{cm} $,$ FC = \frac{1}{2}CD = 2x \, \text{cm} $��。
$ EF = AC - AE - FC = 6x - \frac{3}{2}x - 2x = \frac{5}{2}x \, \text{cm} $�����。
由 $ EF = 10 \, \text{cm} $,得 $ \frac{5}{2}x = 10 $���,解得 $ x = 4 $���。
則 $ AB = 3x = 3×4 = 12 \, \text{cm} $。
答:$ AB $ 的長度為 $ 12 \, \text{cm} $����。