觀察下面的物體,至少添上(
3
)個(gè)相同的正方體可以變成一個(gè)大長(zhǎng)方體;至少去掉(
2
)個(gè)相同的正方體可以變成一個(gè)大長(zhǎng)方體。
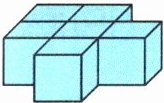
答案:3 2
下圖中的物體是由(
7
)個(gè)小正方體擺成的,至少再添(
20
)個(gè)這樣的正方體,就能變成一個(gè)較大的正方體。
答案:7 20
數(shù)一數(shù),下面的物體是由(
8
)個(gè)同樣大的正方體擺成的,至少添(
8
)個(gè)這樣的正方體就可以變成一個(gè)較大的長(zhǎng)方體。
答案:8 8
例3 用若干個(gè)小正方體拼成立體圖形,使它從前面看到的是,

從右面看到的是,

至少需要(
5
)個(gè)小正方體,最多需要(
7
)個(gè)小正方體。(面與面接觸)
答案:解析:
本題可根據(jù)從前面和右面看到的圖形來確定立體圖形的層數(shù)�、排數(shù)以及每層小正方體的最少和最多數(shù)量,進(jìn)而得出至少和最多需要的小正方體個(gè)數(shù)。
從前面看到的圖形可知,這個(gè)立體圖形有上��、下$2$層,左��、中�����、右$3$列�����;從右面看到的圖形可知����,這個(gè)立體圖形有前、后$2$排���,前面一排有$1$層��,后面一排有$2$層����。
要使小正方體個(gè)數(shù)最少�����,可按如下方式擺放:
第一層(下面一層)前面一排擺$3$個(gè)小正方體,后面一排左側(cè)和中間各擺$1$個(gè)小正方體�����;第二層(上面一層)在后面一排中間位置擺$1$個(gè)小正方體��,這樣共需要$5$個(gè)小正方體�����。
要使小正方體個(gè)數(shù)最多���,在最少個(gè)數(shù)的基礎(chǔ)上�,在下面一層后面一排右側(cè)再增加$2$個(gè)小正方體��,此時(shí)共需要$7$個(gè)小正方體����。
答案:
至少需要$5$個(gè)小正方體,最多需要$7$個(gè)小正方體��。