1.「2024 甘肅甘南州中考」中國(guó)航天取得了舉世矚目的成就,為人類和平貢獻(xiàn)了中國(guó)智慧和中國(guó)力量,下列是有關(guān)中國(guó)航天的圖標(biāo),其文字上方的圖案是中心對(duì)稱圖形的是 (
D
)

答案:期末綜合檢測(cè)
1. D 根據(jù)中心對(duì)稱圖形的定義,可知A,B,C選項(xiàng)不符合題意,D選項(xiàng)符合題意.故選D.
2.跨語文古詩詞「2025 重慶開州期中」下列詩句所描述的事件中,是不可能事件的是 (
A
)
A.手可摘星辰
B.黃河入海流
C.大漠孤煙直
D.魚戲蓮葉東
答案:2. A A.手可摘星辰是不可能事件,符合題意;B.黃河入海流是必然事件,不符合題意;C.大漠孤煙直是隨機(jī)事件,不符合題意;D.魚戲蓮葉東是隨機(jī)事件,不符合題意.故選A.
3.「2024 四川涼山州中考」若關(guān)于 $ x $ 的一元二次方程 $ (a + 2)x^2 + x + a^2 - 4 = 0 $ 的一個(gè)根是 $ x = 0 $,則 $ a $ 的值為 (
A
)
A.2
B.-2
C.2 或-2
D.$\frac{1}{2}$
答案:3. A ∵關(guān)于x的一元二次方程$(a+2)x^{2}+x+a^{2}-4=0$的一個(gè)根是$x=0,\therefore a^{2}-4=0$且$a+2≠0$,解得$a=2$.故選A.
4.「2025 北京大興期末」如圖,在 $ \triangle ABC $ 中,$ \angle CAB = 70^\circ $,在同一平面內(nèi),將 $ \triangle ABC $ 繞點(diǎn) $ A $ 逆時(shí)針旋轉(zhuǎn) $ \alpha $ 得到 $ \triangle AB'C' $,且 $ C'C // AB $,則 $ \alpha $ 的度數(shù)為 (
C
)

A.20°
B.35°
C.40°
D.55°
答案:4. C $\because C'C// AB,\therefore ∠ACC'=∠CAB=70^{\circ },\because $將$△ABC$繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)α得到$△AB'C',\therefore AC=AC'$,$∠BAB'=∠CAC'=α,\therefore ∠ACC'=∠AC'C=70^{\circ },\therefore ∠CAC'=40^{\circ }=α$.故選C.
5.「2024 內(nèi)蒙古赤峰中考」如圖,$ AD $ 是 $ \odot O $ 的直徑,$ AB $ 是 $ \odot O $ 的弦,半徑 $ OC \perp AB $,連接 $ CD $,交 $ OB $ 于點(diǎn) $ E $,$ \angle BOC = 42^\circ $,則 $ \angle OED $ 的度數(shù)是 (
B
)

A.61°
B.63°
C.65°
D.67°
答案:5. B $\because $半徑$OC⊥AB,\therefore \widehat {AC}=\widehat {BC},\therefore ∠AOC=∠BOC=42^{\circ },\therefore ∠D=\frac {1}{2}∠AOC=21^{\circ },\because OC=OD,\therefore ∠C=∠D=21^{\circ },\therefore ∠OED=∠C+∠BOC=21^{\circ }+42^{\circ }=63^{\circ }$.故選B.
6.「2025 遼寧丹東期末」如圖,公園里有一段長(zhǎng) 20 米的墻 $ AB $,工人師傅計(jì)劃利用墻 $ AB $ 和 40 米長(zhǎng)的柵欄圍成一個(gè)面積為 198 平方米的封閉矩形綠化區(qū)域,設(shè)矩形中垂直于墻 $ AB $ 的一邊的柵欄長(zhǎng)為 $ x $ 米,下列說法正確的是 (
C
)

A.$ 2x \cdot (40 - 2x) = 198 $
B.$ x $ 的取值范圍是 $ 0 < x \leq 20 $
C.只有一種圍法
D.有兩種圍法
答案:6. C $\because $垂直于墻的一邊的柵欄長(zhǎng)為x米,$\therefore $平行于墻的一邊的柵欄長(zhǎng)為$(40-2x)$米,則$x(40-2x)=198$,故A錯(cuò)誤;由題意得$\left\{\begin{array}{l} x>0\\ 0<40 - 2x\leq20\end{array}\right. $,解得$10\leq x<20$,故B錯(cuò)誤;對(duì)于方程$x(40-2x)=198$,化簡(jiǎn)得$x^{2}-20x+99=0$,解方程得$x_{1}=9,x_{2}=11,\because 10\leq x<20,\therefore x=11$,故只有一種圍法,故C正確��、D錯(cuò)誤.故選C.
7.「2025 吉林長(zhǎng)春期末」已知一個(gè)二次函數(shù) $ y = ax^2 + bx + c $ 的自變量 $ x $ 與函數(shù) $ y $ 的幾組對(duì)應(yīng)值如表:

則下列關(guān)于這個(gè)二次函數(shù)的結(jié)論正確的是 (
C
)
A.圖象的開口向下
B.表格中 $ m $ 的值大于零
C.函數(shù)的最小值是$-\frac{5}{4}$
D.當(dāng) $ x > 1 $ 時(shí),$ y $ 的值隨 $ x $ 值的增大而增大
答案:7. C 將$(-1,5),(0,1),(1,-1)$代入$y=ax^{2}+bx+c$得$\left\{\begin{array}{l} a - b + c = 5\\ c = 1\\ a + b + c = -1\end{array}\right. $,解得$\left\{\begin{array}{l} a = 1\\ b = -3\\ c = 1\end{array}\right. $,$\therefore y=x^{2}-3x+1$.A.$\because a = 1>0,\therefore $該拋物線開口向上,故該選項(xiàng)結(jié)論錯(cuò)誤,不符合題意;B.當(dāng)$x = 2$時(shí),$y=m=4 - 6 + 1=-1<0$,故該選項(xiàng)結(jié)論錯(cuò)誤,不符合題意;C.$y_{最小值}=\frac {4 - 9}{4}=-\frac {5}{4}$,故該選項(xiàng)結(jié)論正確,符合題意;D.拋物線的對(duì)稱軸為直線$x=\frac {3}{2},\because a = 1>0,\therefore $當(dāng)$x>\frac {3}{2}$時(shí),y隨x的增大而增大,故該選項(xiàng)結(jié)論錯(cuò)誤,不符合題意.故選C.
8.新考向新定義題對(duì)于實(shí)數(shù) $ a,b $ 定義運(yùn)算“$ \otimes $”為 $ a \otimes b = b^2 - ab $,例如 $ 3 \otimes 2 = 2^2 - 3 × 2 = -2 $,則關(guān)于 $ x $ 的方程 $ (k - 3) \otimes x = k - 1 $ 的根的情況,下列說法正確的是 (
A
)
A.有兩個(gè)不相等的實(shí)數(shù)根
B.有兩個(gè)相等的實(shí)數(shù)根
C.無實(shí)數(shù)根
D.無法確定
答案:8. A $\because (k - 3)\otimes x=k - 1,\therefore x^{2}-(k - 3)x=k - 1,\therefore x^{2}-(k - 3)x - k + 1=0,\therefore \Delta=[-(k - 3)]^{2}-4\times1\times(-k + 1)=(k - 1)^{2}+4>0,\therefore $關(guān)于x的方程$(k - 3)\otimes x=k - 1$有兩個(gè)不相等的實(shí)數(shù)根.故選A.
9.「2025 北京通州期末」如圖,已知 $ \odot O $ 及 $ \odot O $ 外一定點(diǎn) $ P $,嘉嘉同學(xué)進(jìn)行了如圖所示的兩步操作后,得出了四個(gè)結(jié)論:
①點(diǎn) $ A $ 是 $ PO $ 的中點(diǎn);
②直線 $ PQ,PR $ 都是 $ \odot O $ 的切線;
③點(diǎn) $ P $ 到點(diǎn) $ Q $、點(diǎn) $ R $ 的距離相等;
④$ S_{\triangle PQA} = \frac{1}{8}S_{四邊形PROQ} $.其中正確的是 (
B
)
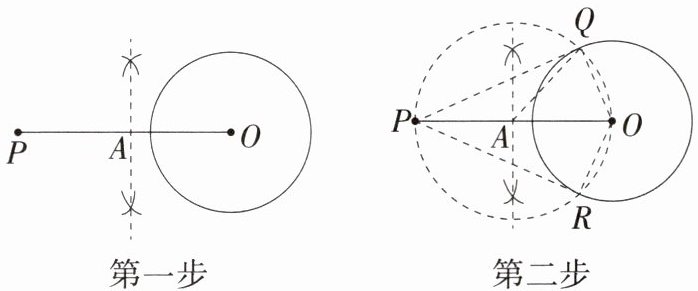
A.①②③④
B.①②③
C.①
D.②
答案:9. B 第一步作出的虛線是線段OP的垂直平分線,∴點(diǎn)A是PO的中點(diǎn),①中結(jié)論正確;第二步中,由圓周角定理可知$∠OQP=∠ORP=90^{\circ },\therefore $直線PQ,PR都是$\odot O$的切線,②中結(jié)論正確;由切線長(zhǎng)定理可知$PQ = PR$,③中結(jié)論正確;由A是PO的中點(diǎn)得$S_{\triangle PQA}=\frac {1}{2}S_{\triangle OQP}$,由題意易得$S_{\triangle POQ}=S_{\triangle POR},\therefore S_{\triangle PQA}=\frac {1}{4}S_{四邊形PROQ}$,④中結(jié)論錯(cuò)誤.故選B.