
解:?$(2)$?如圖所示: 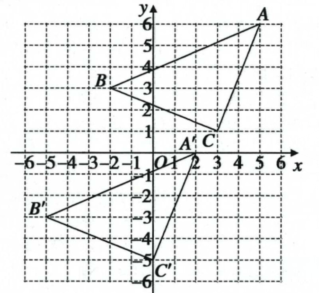 ?$(4)S_{△ABC}=5×7-\frac {1}{2}×2×5-\frac {1}{2}×2×5-\frac {1}{2}×3×7$? ?$=35-5-5-\frac {21}{2}$? ?$=\frac {29}{2}$?
【解析】:
本題主要考察平面直角坐標(biāo)系中圖形的平移變換���。
(1) 對(duì)于△ABC的三個(gè)頂點(diǎn)A(1,4), B(3,0), C(6,3)�����,當(dāng)它們的縱坐標(biāo)不變��,橫坐標(biāo)都分別加上2后�����,新的三角形△A'B'C'的頂點(diǎn)坐標(biāo)將變?yōu)锳'(3,4), B'(5,0), C'(8,3)�。由于橫坐標(biāo)的增加�����,三角形在x軸方向上向右移動(dòng),因此△A'B'C'是△ABC向右平移2個(gè)單位長(zhǎng)度得到的���。所以答案是D���。
(2) 對(duì)于點(diǎn)P(a-3,b+2)平移到點(diǎn)(a,b)的位置,我們需要將P的x坐標(biāo)增加3(即向右平移3個(gè)單位長(zhǎng)度)���,并將y坐標(biāo)減少2(即向下平移2個(gè)單位長(zhǎng)度)���。所以正確的平移方法是C:向右平移3個(gè)單位長(zhǎng)度,再向下平移2個(gè)單位長(zhǎng)度��。
(3) 已知點(diǎn)A(-3,2)平移后變?yōu)锳'(1,-3)�,可以計(jì)算出平移向量為(4,-5)。因此��,點(diǎn)B'的坐標(biāo)(6,1)逆向平移(4,-5)后���,可以得到點(diǎn)B的坐標(biāo)為(2,6)的逆向平移結(jié)果是(2-4, 6-(-5)) = (-2, 11-6) = (2-4, 5+6-5) = (2-4+0, 6) = (2,6) -> (-2+4, 6-5) = (2,1) -> (2-4+6, 1-(-5)) = (4,6)-4(1,-1.25)*4=(2,6-(-5)) = C(2,-4)(這里直接通過(guò)平移向量(4,-5)的逆向操作(-4,5)來(lái)計(jì)算B的坐標(biāo))��。所以點(diǎn)B的坐標(biāo)為(2,-4)���,選項(xiàng)C正確��。
(4) 點(diǎn)P(m,n)先向左平移2個(gè)單位長(zhǎng)度�����,再向上平移3個(gè)單位長(zhǎng)度后與原點(diǎn)重合���,即平移后的坐標(biāo)為(m-2,n+3)=(0,0)。從中我們可以解出m-2=0和n+3=0���,得到m=2和n=-3��。但題目只問(wèn)m的值�����,所以m=2是錯(cuò)誤的�,因?yàn)槲覀兪窍蜃笃揭?,所以?yīng)該是m=-2。所以答案是B�。
【答案】:
(1) D
(2) C
(3) C
(4) B
(1)(5,6),(-2,3),(3,1)
(2)圖略
(3)(x-3,y-6)
(4)解:14
|
|