解:?$(2)$?當(dāng)?$EF $?在點(diǎn)?$C$?的左邊時(shí)���,延長(zhǎng)?$BC$?
交?$EF $?于點(diǎn)?$G�����。$?
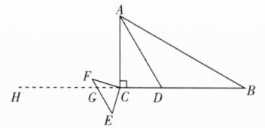
∵?$∠ACB = 90°�,$??$∠B = 30°��,$?
∴?$∠BAC = 60°�。$?
∵?$AD$?是角平分線(xiàn),
∴?$∠CAD=\frac {1}{2}∠BAC = 30°�,$?則
?$∠ADC = 90°-30°=60°。$?
∵?$EF// AD����,$?
∴?$∠FGH=∠ADC = 60°。$?
∵?$∠ECF = 90°�,$??$∠CEF = 45°,$?
∴?$∠CFE = 45°�,$?則
?$∠GCF=∠FGH-∠EFC = 15°,$?
∴?$∠DCF = 180°-∠GCF = 165°�,$?
∴?$t = 165\div 5 = 33$?
當(dāng)?$EF $?在點(diǎn)?$C$?的右邊時(shí),
∵?$∠ACB = 90°���,$??$∠B = 30°��,$?
∴?$∠BAC = 60°����。$?
∵?$AD$?是角平分線(xiàn),
∴?$∠CAD=\frac {1}{2}∠BAC = 30°��,$?則
?$∠ADC = 90°-30°=60°��。$?
∵?$EF// AD��,$?
∴?$∠EGC=∠ADC = 60°����。$?
∵?$∠ECF = 90°����,$??$∠CEF = 45°,$?
∴?$∠CFE = 45°����,$?則
?$∠GCF=∠EGC-∠EFC = 15°。$?
根據(jù)旋轉(zhuǎn)可知�,旋轉(zhuǎn)角為?$360°-15°=345°,$?
∴?$t = 345\div 5 = 69�����。$?
綜上分析可知,?$t = 33$?或?$69$?時(shí)��,使得?$EF// AD����。$?
?$(3)t $?的值為?$9$?或?$18$?或?$54$?或?$63$?