?$(1)$?證明:連接?$OC$?
∵?$OB=OC$?
∴?$∠OCB=∠OBC$?
∵四邊形?$ABCD$?內(nèi)接于?$⊙O$?
∴?$∠OBC+∠ADC=180°$?
∵?$∠ADC+∠CDE=180°$?
∴?$∠CDE=∠OBC$?
∵?$CE⊥AD$?
∴?$∠E=∠CDE+∠ECD=90°$?
∵?$∠ECD=∠BCF$?
∴?$∠OCB+∠BCF=90°$?
∴?$∠OCE=90°,$?即?$OC⊥EF$?
∵?$OC$?是?$⊙O$?的半徑
∴?$CE$?為?$⊙O$?的切線
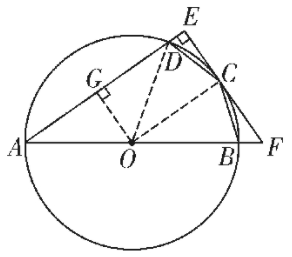
?$(2)$?解:如圖��,過點?$O$?作?$OG⊥AE$?于?$G����,$?連接?$OC,$??$OD��,$?則?$∠OGE=90°$?
∵?$∠E=∠OCE=90°$?
∴四邊形?$OGEC$?是矩形
∴?$OC=EG�����,$??$OG=EC$?
設(shè)?$⊙O$?的半徑為?$x$?
在?$Rt△CDE$?中��,?$CD=3��,$??$DE=1$?
∴?$EC=\sqrt {3^2-1^2}=2\sqrt {2}$?
∴?$OG=2\sqrt {2}��,$??$GD=x-1�����,$??$OD=x$?
由勾股定理得:?$OD^2=OG^2+DG^2$?
∴?$x^2=(2\sqrt {2})^2+(x-1)^2$?
解得:?$x=4.5$?
∴?$⊙O$?的半徑是?$4.5$?