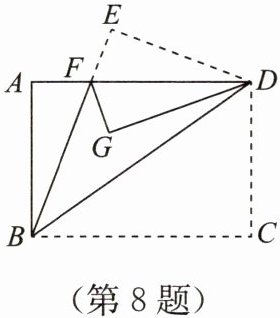
8. 如圖,將一張長方形紙片ABCD沿對角線BD折疊后,點C落在點E處,BE交AD于點F,再將△DEF沿DF折疊后,點E落在點G處,若DG剛好平分∠ADB,則∠BDC的度數(shù)為(
D
).
A.57°
B.56°
C.55°
D.54°
解析:
設(shè)∠BDC=α���。
∵四邊形ABCD是長方形�����,
∴AD//BC����,∠C=90°�,
∴∠ADB=∠DBC。
∵沿對角線BD折疊��,點C落在點E處�����,
∴∠EBD=∠DBC=∠ADB��,∠BED=∠C=90°��,∠EDB=∠BDC=α。
設(shè)∠ADB=β�,則∠EBD=β,∠FDB=β�。
∵∠EDB=α,∠ADB=β��,
∴∠EDF=∠EDB - ∠FDB=α - β��。
將△DEF沿DF折疊����,點E落在點G處�,
∴∠GDF=∠EDF=α - β,∠DGF=∠BED=90°���。
∵DG平分∠ADB���,∠ADB=β,
∴∠ADG=∠GDB=β/2�����。
∵∠GDF=∠EDF=α - β�,∠GDB=β/2��,∠FDB=β���,
∴∠GDF=∠FDB - ∠GDB=β - β/2=β/2,
即α - β=β/2����,得α=3β/2。
在△BDC中�����,∠C=90°��,∠BDC=α�,∠DBC=β,
∴α + β=90°�����,即3β/2 + β=90°����,解得β=36°,
∴α=3β/2=54°��,即∠BDC=54°。
D