5. 小明學(xué)習(xí)了“等式的性質(zhì)”后對(duì)小亮說(shuō):“我發(fā)現(xiàn)$4可以等于3$,你看這里有一個(gè)方程$4x - 2 = 3x - 2$,等式的兩邊都加上$2$,得$4x = 3x$,然后等式的兩邊都除以$x$,得$4 = 3$.”
(1)小明的說(shuō)法對(duì)嗎���?為什么�����?
(2)你能求出方程$4x - 2 = 3x - 2$的解嗎�?
答案:(1)不對(duì).因?yàn)榈仁?x=3x中x的值為0,等式的兩邊不能同時(shí)除以0. (2)方程兩邊都加上2,得4x=3x,然后兩邊都減去3x,得x=0.
問(wèn)題 已知$9m - 3n - 2025 = 0$,試求出$3m - n$的值.
名師指導(dǎo)
先利用等式的性質(zhì)1,在等式兩邊同時(shí)加上$2025$,再利用等式的性質(zhì)2,在等式兩邊同時(shí)除以$3$,即可求出$3m - n$的值.
解題示范(學(xué)生在教師指導(dǎo)下,獨(dú)立完成)
解:
]
答案:解:
由 $9m - 3n - 2025 = 0$,
根據(jù)等式的性質(zhì)1�����,等式兩邊同時(shí)加上$2025$���,得:
$9m - 3n = 2025$���,
再根據(jù)等式的性質(zhì)2,等式兩邊同時(shí)除以$3$���,得:
$\frac{9m - 3n}{3} = \frac{2025}{3}$�����,
即:
$3m - n = 675$���。
1. 方程$1 - 3x = 0$的解是(
B
)
A.$x = -\frac{1}{3}$
B.$x= \frac{1}{3}$
C.$x = -3$
D.$x = 3$
答案:B.
解析:
解:$1 - 3x = 0$
$-3x = -1$
$x = \frac{1}{3}$
B.
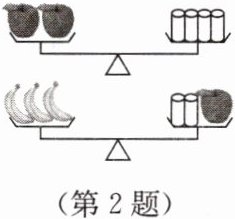
2. 在中央電視臺(tái)“開心辭典”節(jié)目中,某期的一道題目是:如圖,兩個(gè)天平都平衡,則1個(gè)蘋果的重量是1個(gè)香蕉重量的(
C
)
A.$\frac{2}{3}$倍
B.$\frac{4}{3}$倍
C.$\frac{3}{2}$倍
D.$2$倍
]
答案:C.
解析:
設(shè)1個(gè)蘋果的重量為$x$,1個(gè)香蕉的重量為$y$����,1個(gè)砝碼的重量為$z$�。
由第一個(gè)天平:$2x = 4z$��,得$x = 2z$�����。
由第二個(gè)天平:$3y = 2z + x$��,將$x = 2z$代入�,得$3y = 2z + 2z = 4z$,即$y=\frac{4}{3}z$���。
則$\frac{x}{y}=\frac{2z}{\frac{4}{3}z}=\frac{3}{2}$����。
C.
3. 已知等式$3a = 2b + 5$,則下列等式中不成立的是(
C
)
A.$3a - 5 = 2b$
B.$3a + 1 = 2b + 6$
C.$3ac = 2bc + 5$
D.$a= \frac{2}{3}b+\frac{5}{3}$
答案:C.
解析:
A. 由$3a = 2b + 5$���,等式兩邊同時(shí)減5�,得$3a - 5 = 2b$�����,成立��;
B. 由$3a = 2b + 5$�,等式兩邊同時(shí)加1,得$3a + 1 = 2b + 6$�,成立;
C. 由$3a = 2b + 5$�����,等式兩邊同時(shí)乘$c$����,得$3ac = 2bc + 5c$,原選項(xiàng)$3ac = 2bc + 5$不成立���;
D. 由$3a = 2b + 5$�,等式兩邊同時(shí)除以3�����,得$a = \frac{2}{3}b + \frac{5}{3}$�����,成立�����。
C
4. 某城市平均每天產(chǎn)生生活垃圾$700t$,由甲、乙兩個(gè)垃圾處理廠處理.已知甲廠每小時(shí)可處理垃圾$55t$,乙廠每小時(shí)可處理垃圾$45t$.甲�����、乙兩廠同時(shí)處理該城市的生活垃圾,每天需多長(zhǎng)時(shí)間才能處理完��?
答案:7 h.
解析:
設(shè)每天需$x$小時(shí)才能處理完���。
甲廠每小時(shí)處理$55t$��,$x$小時(shí)處理$55x t$��;乙廠每小時(shí)處理$45t$�����,$x$小時(shí)處理$45x t$��。
根據(jù)題意���,可列方程:$55x + 45x = 700$
合并同類項(xiàng)得:$100x = 700$
解得:$x = 7$
7 h.