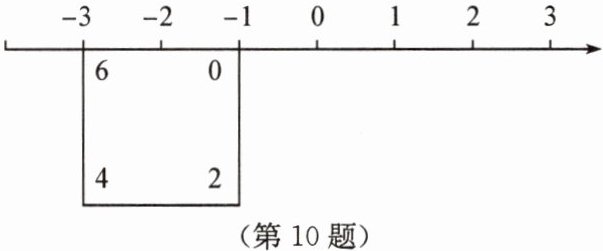
10. 如圖,正方形的周長(zhǎng)為8個(gè)單位長(zhǎng)度.在該正方形的4個(gè)頂點(diǎn)處分別標(biāo)上0,2,4,6,先讓正方形上表示數(shù)字6的點(diǎn)與數(shù)軸上表示-3的點(diǎn)重合,再將數(shù)軸按順時(shí)針方向環(huán)繞在該正方形上,則與數(shù)軸上表示2025的點(diǎn)重合的正方形上的點(diǎn)表示的數(shù)字為(
B
)
A.0
B.2
C.4
D.6
答案:B
解析:
正方形周長(zhǎng)為8,邊長(zhǎng)為2��,數(shù)字0,2,4,6按順時(shí)針排列���。6與-3重合���,數(shù)軸順時(shí)針環(huán)繞,周期為8�����。
2025 - (-3) = 2028��,2028 ÷ 8 = 253……4,余數(shù)為4��。
從6開始順時(shí)針數(shù)4個(gè)單位:6→0→2→4→6�,第4個(gè)為2。
B
11. 若x,y互為倒數(shù),則$(-xy)^{2026}=$
1
.
答案:1
解析:
因?yàn)?x$����,$y$互為倒數(shù),所以$xy = 1$����。
則$(-xy)^{2026}=(-1)^{2026}=1$。
1
12. 某日北京市的最低氣溫為-3℃,武漢市的最低氣溫為5℃,這一天北京市的最低氣溫比武漢市的最低氣溫低
8
℃.
答案:8
13. 在-0.4217中用數(shù)字3替換其中的一個(gè)非零數(shù)字,使所得的數(shù)最小,則被替換的數(shù)字是
2
.
答案:2
解析:
將-0.4217中的非零數(shù)字4����、2、1�、7分別替換為3,得到:
-0.3217����,-0.4317,-0.4237�����,-0.4213。
比較大?�。?0.4317 < -0.4237 < -0.4213 < -0.3217�。
最小的數(shù)是-0.4317,被替換的數(shù)字是2����。
2
14. 寫出系數(shù)是-2,且只含有字母a,b的所有3次單項(xiàng)式:
$-2a^{2}b$,$-2ab^{2}$
.
答案:$-2a^{2}b$��,$-2ab^{2}$
15. 已知a+b= 8,則代數(shù)式1-2a-2b的值為
-15
.
答案:$-15$
解析:
$1 - 2a - 2b = 1 - 2(a + b)$��,
因?yàn)?a + b = 8$�����,
所以原式$= 1 - 2×8 = 1 - 16 = -15$��。
$-15$
16. 數(shù)學(xué)課上老師講了合并同類項(xiàng),小玉回到家后拿出自己的課堂筆記,認(rèn)真地復(fù)習(xí)老師在課堂上所講的內(nèi)容,她突然發(fā)現(xiàn)了一道題目:$(2a^2+3ab-b^2)-(-3a^2+ab+5b^2)= 5a^2$
+2ab
-6b^2,其中的一項(xiàng)被墨水弄臟了,則被墨水弄臟的一項(xiàng)是______.

答案:$+2ab$
解析:
$(2a^2 + 3ab - b^2) - (-3a^2 + ab + 5b^2)$
$=2a^2 + 3ab - b^2 + 3a^2 - ab - 5b^2$
$=(2a^2 + 3a^2) + (3ab - ab) + (-b^2 - 5b^2)$
$=5a^2 + 2ab - 6b^2$
$+2ab$
17. 當(dāng)k=
-1
時(shí),多項(xiàng)式$x^2-(k-1)xy-3y^2-2xy-5$中不含xy項(xiàng).
答案:$-1$
解析:
多項(xiàng)式$x^2-(k-1)xy-3y^2-2xy-5$合并同類項(xiàng)���,得:
$x^2+[-(k-1)-2]xy-3y^2-5$
$=x^2+(-k+1-2)xy-3y^2-5$
$=x^2+(-k-1)xy-3y^2-5$
因?yàn)槎囗?xiàng)式不含$xy$項(xiàng),所以$-k - 1 = 0$��,解得$k=-1$���。
$-1$
18. 數(shù)軸上在原點(diǎn)左邊且距離原點(diǎn)2個(gè)單位長(zhǎng)度的點(diǎn)所表示的數(shù)是
$-2$
.
答案:$-2$
19. 已知$|x|= 7$,$|y|= 9$,且$|x-y|= y-x$,則$y^2+2x= $
95或67
.
答案:95或67
解析:
因?yàn)?|x| = 7$����,所以$x = \pm 7$;因?yàn)?|y| = 9$�����,所以$y = \pm 9$�����。
又因?yàn)?|x - y| = y - x$����,所以$y - x \geq 0$,即$y \geq x$����。
當(dāng)$y = 9$時(shí):
若$x = 7$,滿足$9 \geq 7$�,此時(shí)$y^2 + 2x = 9^2 + 2×7 = 81 + 14 = 95$;
若$x = -7$���,滿足$9 \geq -7$��,此時(shí)$y^2 + 2x = 9^2 + 2×(-7) = 81 - 14 = 67$�����。
當(dāng)$y = -9$時(shí)�����,無論$x = 7$還是$x = -7$��,都有$-9 < 7$且$-9 < -7$��,不滿足$y \geq x$����,故舍去��。
綜上�,$y^2 + 2x = 95$或$67$。
95或67
20. 按如圖所示的程序計(jì)算,若開始輸入的x的值為30,第1次得到的結(jié)果為15,第2次得到的結(jié)果為24……第2025次得到的結(jié)果為
12
.

答案:12
解析:
第1次:30為偶數(shù)����,結(jié)果為$\frac{1}{2}×30 = 15$
第2次:15為奇數(shù),結(jié)果為$15 + 9 = 24$
第3次:24為偶數(shù),結(jié)果為$\frac{1}{2}×24 = 12$
第4次:12為偶數(shù)��,結(jié)果為$\frac{1}{2}×12 = 6$
第5次:6為偶數(shù)���,結(jié)果為$\frac{1}{2}×6 = 3$
第6次:3為奇數(shù)����,結(jié)果為$3 + 9 = 12$
第7次:12為偶數(shù)�,結(jié)果為$\frac{1}{2}×12 = 6$
第8次:6為偶數(shù),結(jié)果為$\frac{1}{2}×6 = 3$
第9次:3為奇數(shù)��,結(jié)果為$3 + 9 = 12$
……
從第3次開始����,結(jié)果以12,6���,3循環(huán)�,周期為3
$(2025 - 2)÷3 = 2023÷3 = 674\cdots\cdots1$���,余數(shù)為1
第2025次得到的結(jié)果為12
21. (12分)計(jì)算:
(1)$(-3)^3÷2\frac{1}{4}+4-2^2×(-\frac{1}{3})$��;
(2)$(\frac{1}{8}+1\frac{1}{3}-2.75)×(-24)+(-1)^{2026}$�����;
(3)$3(m-2n)-2(-2n+3m)$�����;
(4)$-5(a^2b-2ab^2)+3(3b^2a-2ba^2)$.
答案:(1)$-6\frac{2}{3}$��;(2)32��;(3)$-3m-2n$��;(4)$-11a^{2}b+19ab^{2}$
解析:
(1) $(-3)^3÷2\frac{1}{4}+4-2^2×(-\frac{1}{3})$
$=-27÷\frac{9}{4}+4-4×(-\frac{1}{3})$
$=-27×\frac{4}{9}+4+\frac{4}{3}$
$=-12+4+\frac{4}{3}$
$=-8+\frac{4}{3}$
$=-\frac{24}{3}+\frac{4}{3}$
$=-\frac{20}{3}=-6\frac{2}{3}$
(2) $(\frac{1}{8}+1\frac{1}{3}-2.75)×(-24)+(-1)^{2026}$
$=(\frac{1}{8}+\frac{4}{3}-\frac{11}{4})×(-24)+1$
$=\frac{1}{8}×(-24)+\frac{4}{3}×(-24)-\frac{11}{4}×(-24)+1$
$=-3-32+66+1$
$=(-3-32)+(66+1)$
$=-35+67=32$
(3) $3(m-2n)-2(-2n+3m)$
$=3m-6n+4n-6m$
$=(3m-6m)+(-6n+4n)$
$=-3m-2n$
(4) $-5(a^2b-2ab^2)+3(3b^2a-2ba^2)$
$=-5a^2b+10ab^2+9ab^2-6a^2b$
$=(-5a^2b-6a^2b)+(10ab^2+9ab^2)$
$=-11a^2b+19ab^2$