6. (2023·淮安淮陰期中)如圖,C是線段BG上的一點,以BC,CG為邊向兩A
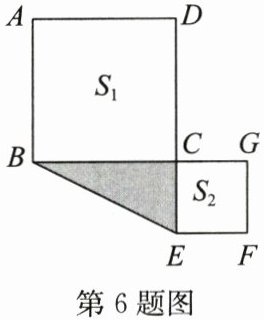
邊作正方形,面積分別是$S_{1}和S_{2}$,兩個正方形的面積和$S_{1}+S_{2}= 20$,已知BG= 6,則圖中陰影部分的面積為(
A
)
A.4
B.6
C.7
D.8
解析:
設(shè)正方形$ABCD$的邊長為$a$����,正方形$CEFG$的邊長為$b$。
因為$S_{1}$和$S_{2}$分別是兩個正方形的面積����,所以$S_{1}=a^{2}$,$S_{2}=b^{2}$��。已知$S_{1}+S_{2}=20$���,則$a^{2}+b^{2}=20$���。
又因為$BG=6$���,且$BG=BC + CG=a + b$�,所以$a + b=6$�����。
對$(a + b)^{2}$進行展開可得$(a + b)^{2}=a^{2}+2ab + b^{2}$,將$a + b=6$��,$a^{2}+b^{2}=20$代入可得:
$6^{2}=20 + 2ab$
$36=20 + 2ab$
$2ab=36 - 20$
$2ab=16$
$ab=8$
由圖可知����,陰影部分是一個三角形,其底為$a$���,高為$b$����,所以陰影部分的面積為$\frac{1}{2}ab$��。
將$ab=8$代入可得:$\frac{1}{2}×8 = 4$����。
故答案為A。