1.如圖,四個圖案具有一個共有的性質(zhì),則下面四個數(shù)字中,滿足上述性質(zhì)的是 (
C
)
A.6
B.7
C.8
D.9
答案:C
2.如圖,在等腰三角形ABC中,$AB= AC,∠BAC= 40^{\circ }$,中線AD與角平分線CE交于點F,則$∠CFD$的度數(shù)為 (
B
)
A.$25^{\circ }$
B.$35^{\circ }$
C.$45^{\circ }$
D.$55^{\circ }$
答案:1. 首先�����,根據(jù)等腰三角形的性質(zhì):
因為$AB = AC$���,$AD$是中線����,根據(jù)等腰三角形“三線合一”(等腰三角形底邊上的高�����、底邊上的中線����、頂角平分線互相重合),所以$AD\perp BC$�����,即$\angle ADC = 90^{\circ}$�。
又因為$AB = AC$�����,$\angle BAC=40^{\circ}$����,根據(jù)三角形內(nèi)角和定理$\angle B+\angle ACB+\angle BAC = 180^{\circ}$��,且$\angle B=\angle ACB$����,則$\angle ACB=\frac{1}{2}(180^{\circ}-\angle BAC)$�。
把$\angle BAC = 40^{\circ}$代入$\angle ACB=\frac{1}{2}(180^{\circ}-\angle BAC)$,可得$\angle ACB=\frac{1}{2}(180 - 40)^{\circ}=70^{\circ}$��。
2. 然后�,因為$CE$是角平分線:
所以$\angle ECB=\frac{1}{2}\angle ACB$(角平分線定義)。
把$\angle ACB = 70^{\circ}$代入$\angle ECB=\frac{1}{2}\angle ACB$���,得$\angle ECB=\frac{1}{2}×70^{\circ}=35^{\circ}$�����。
3. 最后��,在$\triangle DFC$中:
根據(jù)三角形外角的性質(zhì)(三角形的一個外角等于與它不相鄰的兩個內(nèi)角之和)�����,在$\triangle DFC$中��,$\angle CFD+\angle FCD=\angle ADC$���。
已知$\angle ADC = 90^{\circ}$����,$\angle FCD=\angle ECB = 35^{\circ}$�����,則$\angle CFD=\angle ADC-\angle FCD$����。
所以$\angle CFD=90^{\circ}-35^{\circ}=35^{\circ}$。
綜上���,答案是B�。
解析:
在等腰△ABC中����,AB=AC�����,∠BAC=40°�,
∴∠ABC=∠ACB=(180°-40°)/2=70°��。
∵CE是角平分線���,
∴∠ACE=∠ACB/2=35°�����。
∵AD是中線,AB=AC��,
∴AD平分∠BAC�����,∠BAD=∠CAD=40°/2=20°�。
在△AFC中,∠AFC=180°-∠CAD-∠ACE=180°-20°-35°=125°��。
∵∠CFD+∠AFC=180°,
∴∠CFD=180°-125°=55°��。
D
3.如圖,在$\triangle ABC$中,E是BC上一點,$AE= AB$,EF垂直平分AC,$AD⊥BC$于點D.若$\triangle ABC$的周長為18 cm,$AC= 7cm$,則DC的長為 (
C
)
A.4.5 cm
B.5 cm
C.5.5 cm
D.6 cm
答案:C
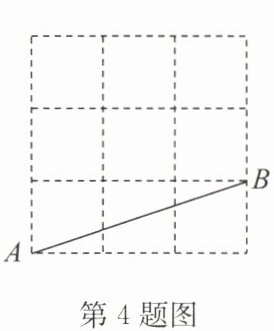
4.(2024春·牡丹區(qū)期末)如圖,在正方形網(wǎng)格內(nèi),A,B兩點都在小正方形的頂點上,如果點C也是圖中小正方形的頂點,且$\triangle ABC$是等腰三角形,那么點C的個數(shù)為 (
C
)
A.1
B.2
C.3
D.4
答案:C
解析:
以A為頂點:AB為腰�����,在網(wǎng)格中找到與B關(guān)于A對稱或滿足AC=AB的點���,無符合條件的點����。
以B為頂點:BA為腰����,同理,無符合條件的點�。
以C為頂點:CA=CB,作AB的垂直平分線�,與網(wǎng)格頂點交于3個點。
綜上��,點C的個數(shù)為3�。
C
5.若點$P(m-1,5)與點Q(3,2-n)$關(guān)于y軸對稱,則$m+n$的值是
?5
.
答案:?5
解析:
因為點$P(m - 1,5)$與點$Q(3,2 - n)$關(guān)于$y$軸對稱,所以橫坐標互為相反數(shù),縱坐標相等�����。
可得:$m - 1 = -3$����,$2 - n = 5$。
由$m - 1 = -3$�,解得$m = -3 + 1 = -2$。
由$2 - n = 5$�����,解得$n = 2 - 5 = -3$�����。
則$m + n = -2 + (-3) = -5$��。
$-5$
6.已知等腰三角形的兩邊長分別為x和y,且x和y滿足$|x-3|+(y-1)^{2}= 0$,則這個等腰三角形的周長為
7
.
答案:7
解析:
因為$|x - 3| + (y - 1)^2 = 0$�,絕對值和平方數(shù)具有非負性����,所以$x - 3 = 0$,$y - 1 = 0$,解得$x = 3$���,$y = 1$����。
等腰三角形的兩邊長為$3$和$1$�����,分兩種情況:
當腰長為$1$時���,三邊長為$1$�����,$1$��,$3$��。因為$1 + 1 = 2 < 3$���,不滿足三角形兩邊之和大于第三邊,所以這種情況不成立�。
當腰長為$3$時,三邊長為$3$,$3$��,$1$��。因為$3 + 1 = 4 > 3$����,$3 + 3 = 6 > 1$,滿足三角形三邊關(guān)系�����,此時周長為$3 + 3 + 1 = 7$���。
7
7.如圖,在$\triangle ABC$中,$AB= AC,AD⊥BC$于點D,$DE⊥AC$于點E,$CF⊥AB$于點F.若$DE= 4$,則CF的長為______
8
.
答案:8
解析:
連接DF�,設(shè)AB=AC=2a����。
∵AB=AC,AD⊥BC����,
∴BD=DC,∠BAD=∠CAD�。
∵DE⊥AC,CF⊥AB����,
∴∠AED=∠AFC=90°。
在△ADE和△AFC中��,∠DAE=∠CAF��,∠AED=∠AFC�,
∴△ADE∽△AFC,$\frac{DE}{CF}=\frac{AD}{AC}$����。
∵AD⊥BC,DE⊥AC�����,
∴△ADE∽△ACD�,$\frac{AD}{AC}=\frac{AE}{AD}$,即$AD^2=AE\cdot AC$���。
設(shè)AE=x�����,則$AD^2=2a\cdot x$����。
在Rt△ADE中,$AD^2=AE^2+DE^2=x^2+16$��,
∴$2a\cdot x=x^2+16$����。
又
∵S△ADC=$\frac{1}{2}AD\cdot DC=\frac{1}{2}AC\cdot DE$,$DC=\sqrt{AC^2-AD^2}=\sqrt{4a^2-(x^2+16)}$�,
$\frac{1}{2}AD\cdot DC=\frac{1}{2}\cdot 2a\cdot 4=4a$,即$AD\cdot DC=8a$�����。
$AD^2\cdot DC^2=64a^2$�����,$(x^2+16)(4a^2-x^2-16)=64a^2$���。
由$2a\cdot x=x^2+16$得$x=\frac{x^2+16}{2a}$���,代入上式化簡得$a=2x$�����。
則$AD^2=2a\cdot x=4x^2$,$AD=2x$�����。
在Rt△ADE中����,$AD^2=AE^2+DE^2$,$4x^2=x^2+16$���,$x^2=\frac{16}{3}$�����,$AD=2x=\frac{8\sqrt{3}}{3}$���,$AC=2a=4x=\frac{16\sqrt{3}}{3}$。
$\frac{DE}{CF}=\frac{AD}{AC}=\frac{1}{2}$�����,
∴CF=2DE=8。
8
8.如圖,在$\triangle ABC$中,AD平分$∠BAC,CD⊥AD$.若$∠ABC與∠ACD$互補,$CD= 5$,則BC的長為
10
.
答案:10
解析:
延長CD交AB于點E��。
∵AD平分∠BAC��,
∴∠EAD=∠CAD�。
∵CD⊥AD,
∴∠ADE=∠ADC=90°�����。
在△ADE和△ADC中����,
∠EAD=∠CAD,AD=AD��,∠ADE=∠ADC���,
∴△ADE≌△ADC(ASA)���。
∴DE=CD=5,∠AED=∠ACD�����。
∴CE=CD+DE=10。
∵∠ABC與∠ACD互補����,∠AED=∠ACD,
∴∠ABC+∠AED=180°��。
∵∠AED+∠BEC=180°����,
∴∠ABC=∠BEC���。
∴BC=CE=10����。
10
9.如圖,在銳角三角形ABC中,$∠A= 30^{\circ },BC= 3,S_{\triangle ABC}= 8$,P是邊BC上的一動點,點P關(guān)于直線AB,AC的對稱點分別是M,N,連接MN,則MN的最小值為______
$\frac{16}{3}$
.
答案:$\frac{16}{3}$
解析:
連接AM�、AN、AP���,過點B作BD⊥AC于點D��。
在Rt△ABD中�,∠A=30°�����,設(shè)BD=h,則AB=2h�����。
S△ABC=$\frac{1}{2}×AC×BD$=8��,即$\frac{1}{2}×AC×h$=8���,得AC×h=16���。
點P關(guān)于AB、AC的對稱點為M�����、N�,
∴AM=AP,AN=AP�����,∠MAB=∠PAB,∠NAC=∠PAC����。
∠MAN=∠MAB+∠PAB+∠NAC+∠PAC=2(∠PAB+∠PAC)=2∠BAC=60°。
∴△AMN是等邊三角形��,MN=AM=AP��。
當AP⊥BC時���,AP最小���。
S△ABC=$\frac{1}{2}×BC×AP$=8���,BC=3���,
∴$\frac{1}{2}×3×AP$=8,AP=$\frac{16}{3}$���。
MN的最小值為$\frac{16}{3}$���。