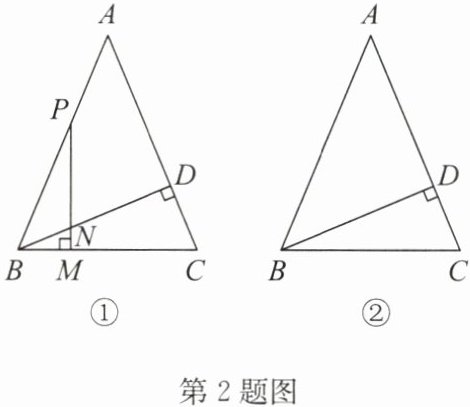
2. 如圖①,在$\triangle ABC$中,$AB= AC,∠BAC= 45^{\circ },BD⊥AC$,P為邊AB上一點(不與點A,B重合),$PM⊥BC$,垂足為M,交BD于點N.
(1)試猜想PN與BM之間的數(shù)量關(guān)系,并證明.
(2)若P為邊AB延長線上一點,$PM⊥BC$所在直線,垂足為M,交DB的延長線于點N,請在圖②中畫出圖形,并判斷(1)中的結(jié)論是否成立.若成立,請證明;若不成立,請寫出你的猜想并證明.
類型二 利用“角平分線+平行線”構(gòu)造等腰三角形
方法技巧:有角平分線時,常過角平分線上一點作角的一邊的平行線,從而構(gòu)造等腰三角形.
基本圖形:如圖,若$∠1= ∠2,AC// OB$,則$\triangle OAC$為等腰三角形.

答案:解:
(1)PN=2BM.證明如下:
如答圖①,作PF//AC交BC于點F,交BD于點E.
∵BD⊥AC,PF//AC,
∴PF⊥BD,∠BPE=∠A=45°,
∴∠BEP=90°,∠PBE=∠BPE=45°,
∴BE=PE.
∵PM⊥BC,
∴∠PMB=∠PEN=90°.
∵∠BNM=∠PNE,
∴∠NPE=∠EBF;
∵∠PEN=∠BEF=90°,
∴△PEN≌△BEF(ASA),
∴PN=BF;
∵AB=AC,
∴∠ABC=∠C;
∵PF//AC,
∴∠PFB=∠C,
∴∠PFB=∠PBF,
∴PB=PF.
∵PM⊥BF,
∴BM=MF,
∴PN=2BM;
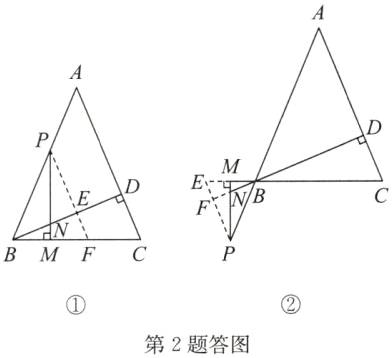
(2)結(jié)論成立.證明如下:
如答圖②,作PE//AC交CM的延長線于點E,交DN的延長線于點F.
∵PF//AC,BD⊥AC,
∴BF⊥EP.
∴∠ABD=∠PBF=∠BPF=45°,
∴BF=PF;
∵∠E+∠EBF=90°,∠E+∠EPM=90°,
∴∠EBF=∠EPM;
∵∠EFB=∠NFP,BF=PF,
∴△BFE≌△PFN(ASA),
∴BE=PN;
∵∠E=∠C=∠ABC=∠PBE,
∴PE=PB.
∵PM⊥EB,
∴EM=BM,
∴PN=2BM.