1. 生物小組的同學想用 18 m 長的籬笆圍成一個等腰三角形區(qū)域作為苗圃. 如果苗圃的一邊長是4m,那么苗圃的另外兩邊長分別是 (
C
)
A.4 m,4 m
B.4 m,10 m
C.7 m,7 m
D.7 m,7 m 或 4 m,10 m
答案:C
解析:
情況1:若4m為腰長���,則底邊長為18-4-4=10m����。因為4+4=8<10��,不滿足三角形兩邊之和大于第三邊�,舍去。
情況2:若4m為底邊長��,則腰長為(18-4)÷2=7m�。因為7+7=14>4,7+4=11>7��,滿足三角形三邊關(guān)系���。
C
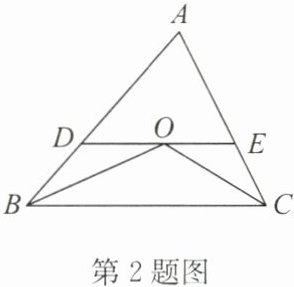
2. 如圖,在$\triangle ABC$中,$AB= BC,BO,CO分別平分∠ABC和∠ACB$,過點O作$DE// BC$,分別交邊 AB,AC 于點 D,E. 如果$\triangle ABC$的周長為 14,$\triangle ADE$的周長為 9,那么 AC 的長為______
4
.
答案:4
解析:
∵BO平分∠ABC�����,
∴∠ABO=∠CBO��,
∵DE//BC���,
∴∠DOB=∠CBO,
∴∠ABO=∠DOB�����,
∴BD=OD,
同理可得CE=OE����,
∵△ADE的周長為9,
∴AD+DE+AE=AD+DO+OE+AE=AD+BD+CE+AE=AB+AC=9����,
∵△ABC的周長為14,
∴AB+BC+AC=14����,
∵AB=BC,
∴AB+AB+AC=14���,
即2AB+AC=14�,
又
∵AB+AC=9���,
∴AB=14-9=5�,
∴AC=9-AB=9-5=4.
4
3. 如圖,在$\triangle ABC$中,$BC= 8,∠B= 2∠C$,D 為邊 AC 的垂直平分線與邊 BC 的交點,且$BD= AB-2.$
(1)求證:$AB= AD;$
(2)求 CD 的長.

答案:
(1)證明:
∵D為邊AC的垂直平分線與邊BC的交點��,
∴DC=AD,
∴∠C=∠CAD,
∴∠ADB=∠C+∠CAD=2∠C=∠B,
∴AB=AD.
(2)解:
∵AB=AD,CD=AD,BD=AB?2,BC=8,
∴CD+CD?2=8,
∴CD=5.
4. 如圖,已知$\triangle ABC$,給出下列四組條件:①在$\triangle ABC$中,$AB= AC$;②在$\triangle ABC$中,$∠B= 56^{\circ },$$∠BAC= 68^{\circ }$;③在$\triangle ABC$中,$AD⊥BC$,AD 平分$∠BAC$;④在$\triangle ABC$中,$AD⊥BC$,AD 平分邊 BC. 其中能判定$\triangle ABC$是等腰三角形的共有 (
D
)
A.1組
B.2組
C.3組
D.4組
答案:D
解析:
①在$\triangle ABC$中,$AB=AC$����,根據(jù)等腰三角形定義,$\triangle ABC$是等腰三角形�����;
②在$\triangle ABC$中�,$\angle B=56^{\circ}$����,$\angle BAC=68^{\circ}$,則$\angle C=180^{\circ}-\angle B-\angle BAC=180^{\circ}-56^{\circ}-68^{\circ}=56^{\circ}$�����,$\angle B=\angle C$����,所以$AB=AC$,$\triangle ABC$是等腰三角形�;
③在$\triangle ABC$中,$AD\perp BC$��,$AD$平分$\angle BAC$,則$\angle BAD=\angle CAD$��,$\angle ADB=\angle ADC=90^{\circ}$��,$AD=AD$�����,$\triangle ABD\cong\triangle ACD(ASA)$�����,$AB=AC$�,$\triangle ABC$是等腰三角形;
④在$\triangle ABC$中��,$AD\perp BC$��,$AD$平分邊$BC$�����,則$BD=CD$�,$\angle ADB=\angle ADC=90^{\circ}$,$AD=AD$���,$\triangle ABD\cong\triangle ACD(SAS)$�����,$AB=AC$�,$\triangle ABC$是等腰三角形;
能判定$\triangle ABC$是等腰三角形的共有4組�����。
D
5. (2024 春·青山區(qū)期末)如圖,在$3×3$的網(wǎng)格中,以 AB 為一邊,點 P 在格點處,使$\triangle ABP$為等腰三角形的點 P 有 (
A
)
A.5個
B.3個
C.2個
D.1個
答案:A
解析:
以AB為腰:
以A為圓心���,AB長為半徑畫圓,與格點交于3個點����;
以B為圓心,AB長為半徑畫圓�,與格點交于2個點。
以AB為底邊:
作AB的垂直平分線�,與格點交于0個點。
共3+2+0=5個點���。
A