1. (1)【觀察思考】如圖,線段AB上有兩個點C,D,請分別寫出以點A,B,C,D為端點的線段,并計算圖中共有多少條線段;
(2)【模型構(gòu)建】如果線段上有m個點(包括線段的兩個端點),則該線段上共有多少條線段? 請說明你結(jié)論的正確性;
(3)【拓展應(yīng)用】8位同學(xué)參加班上組織的象棋比賽,比賽采用單循環(huán)制(即每兩位同學(xué)之間都要進行一場比賽),那么一共要進行多少場比賽?

答案:1.解:(1)以點 A 為左端點,向右的線段有線段 AB��、線段 AC�����、線段 AD����;
以點 C 為左端點,向右的線段有線段 CD�、線段 CB;
以點 D 為左端點的線段有線段 DB.
一共有 3+2+1=6(條)線段.
(2)一共有$\frac {m(m-1)}{2}$條線段.理由如下:
設(shè)線段上有 m 個點,該線段上共有線段 x 條,
則$x=(m-1)+(m-2)+(m-3)+\cdots +3+2+1,$
倒序排列$x=1+2+3+\cdots +(m-3)+(m-2)+(m-1),$
$\therefore 2x=\underbrace{m+m+\cdots +m}_{(m-1)個m}=m(m-1),$
$\therefore x=\frac {m(m-1)}{2}.$
(3)把 8 位同學(xué)看作直線上的 8 個點,每兩位同學(xué)之間的一場比賽看作一條線段,
直線上 8 個點所構(gòu)成的線段條數(shù)就等于比賽的場數(shù).
因此一共要進行$\frac {8×(8-1)}{2}=28$(場)比賽.
2. (2024秋·阜陽期中)解答下列各題:
(1)如圖,在$\angle AOB$中,以O(shè)為頂點引射線,補充完整下表:
| $\angle AOB$內(nèi)射線的條數(shù) | 1 | 2 | 3 | 4 |
| 角的總個數(shù) | | | | |
(2)若$\angle AOB$內(nèi)射線的條數(shù)是n,請用含n的式子表示上面的結(jié)論;
(3)若$\angle AOB$內(nèi)射線的條數(shù)是2025,則角的總個數(shù)是多少?

答案:2.解:(1)填表如下:
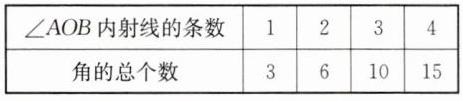
(2)若$\angle AOB$內(nèi)射線的條數(shù)是n,則角的總個數(shù)為$\frac {1}{2}(n+$1)$(n+2).$
(3)當$n=2025$時,
$\frac {1}{2}(n+1)(n+2)=\frac {1}{2}×2026×2027=2053351.$
即角的總個數(shù)為 2053351.