1.(2024 秋·高郵期中)下列各組數(shù)中,互為倒數(shù)的是 (
C
)
A.2 和 -2
B.3 和 $-\frac{1}{3}$
C.-3 和 $-\frac{1}{3}$
D.0 和 0
答案:C
解析:
A. $2 × (-2) = -4 \neq 1$,不是互為倒數(shù)�;
B. $3 × \left(-\frac{1}{3}\right) = -1 \neq 1$,不是互為倒數(shù)��;
C. $-3 × \left(-\frac{1}{3}\right) = 1$���,是互為倒數(shù);
D. 0沒有倒數(shù)。
C
2.(2024 秋·海珠區(qū)期中)下列化簡正確的是 (
B
)
A.$\frac{-13}{-3}= -4$
B.$-\frac{10}{5}= -2$
C.$\frac{-75}{0}= 0$
D.$\frac{-18}{12}= \frac{3}{2}$
答案:B
解析:
A.$\frac{-13}{-3}=\frac{13}{3}\neq -4$
B.$-\frac{10}{5}=-2$
C.分母不能為0�,無意義
D.$\frac{-18}{12}=-\frac{3}{2}\neq \frac{3}{2}$
結(jié)論:B
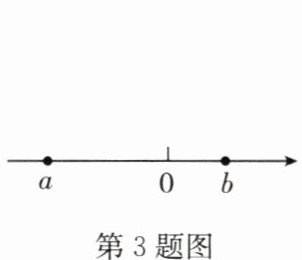
3.(2024 秋·順德區(qū)期中)有理數(shù) a,b 對應(yīng)的點在數(shù)軸上的位置如圖所示,則 (
C
)
A.$a>0$
B.$a+b>0$
C.$a-b<0$
D.$ab>0$
答案:C
解析:
由數(shù)軸可知:$a < 0$,$b > 0$��,且$|a| > |b|$�。
A選項:$a < 0$,故A錯誤����。
B選項:$a + b < 0$,故B錯誤�。
C選項:$a - b = a + (-b) < 0$,故C正確����。
D選項:$ab < 0$,故D錯誤�。
C
4. 如圖是一個數(shù)值轉(zhuǎn)換機,按圖中的運算過程輸入一個數(shù) x. 若輸入的數(shù) $x= -1$,則輸出的結(jié)果為 (
C
)
A.15
B.13
C.11
D.-5
答案:C
解析:
輸入$x = -1$,計算$(-1)×(-2)+1 = 2 + 1 = 3$���,$3 < 10$����;將$3$作為新的$x$輸入��,計算$3×(-2)+1 = -6 + 1 = -5$��,$-5 < 10$����;將$-5$作為新的$x$輸入,計算$(-5)×(-2)+1 = 10 + 1 = 11$�����,$11 > 10$���,輸出結(jié)果為$11$���。
C
5.(2024 秋·如東縣期中)計算 $\left|-\frac{3}{4}\right| ×(-4)$ 的結(jié)果為
-3
.
答案:-3
解析:
$\left|-\frac{3}{4}\right| ×(-4)=\frac{3}{4}×(-4)=-3$
6. 把 $8-(+11)-(-20)+(-19)$ 改寫成省略加號和括號的形式:
8-11+20-19
.
答案:8-11+20-19
7.(2024 秋·江都區(qū)期中)已知 a 是最大的負整數(shù),b 是最小的正整數(shù),c 是絕對值最小的數(shù),則 $a+c-b= $
-2
.
答案:-2
解析:
a是最大的負整數(shù),所以$a=-1$����;b是最小的正整數(shù),所以$b=1$�����;c是絕對值最小的數(shù)�,所以$c=0$����。則$a+c-b=-1+0-1=-2$��。
$-2$
8.(2024·陜西)小華探究“幻方”時,提出了一個問題:如圖,將 0,-2,-1,1,2 這五個數(shù)分別填在五個小正方形內(nèi),使橫向三個數(shù)之和與縱向三個數(shù)之和相等,則填入中間位置的小正方形內(nèi)的數(shù)可以是
0
.(寫出一個符合題意的數(shù)即可)
答案:0(答案不唯一)
9.(20 分)計算:
(1)$32+(-18)+18-29$��; (2)$-63 ÷ 7+45 ÷(-9)$�;
(3)$\frac{6}{19} ÷\left(-1 \frac{1}{2}\right) × \frac{19}{24}$; (4)$\left[1 \frac{1}{24}-\left(\frac{3}{8}+\frac{1}{6}-\frac{3}{4}\right) × 24\right] ÷(-5)$.
答案:解:(1)原式=32+(-18+18)-29=32-29=3. (2)原式=-9+(-5)=-14. (3)原式=$-\frac{6}{19}×\frac{2}{3}×\frac{19}{24}=-\frac{1}{6}$. (4)原式=$[1\frac{1}{24}-(9+4-18)]÷(-5)$=$(1\frac{1}{24}+5)÷(-5)=-\frac{5}{24}-1=-1\frac{5}{24}$.