亚洲精品国产精品乱码不卡√,无码内射成人免费喷射

11. 一個兩位數(shù),個位上的數(shù)字與十位上的數(shù)字之和是 12,將兩個數(shù)字對調(diào)后得到的兩位數(shù)為原來兩位數(shù)的 $ \frac{4}{7} $,則原來的兩位數(shù)是

答案：84 解析:設(shè)原來的兩位數(shù)十位上的數(shù)字$x$，那么個位上的數(shù)字為$12 - x$，由題意得$\frac{4}{7}[10x+(12 - x)] = 10(12 - x)+x$，解得$x = 8$，$12 - x = 4$，所以原來的兩位數(shù)是84。

解析：

解：設(shè)原來的兩位數(shù)十位上的數(shù)字為$x$，則個位上的數(shù)字為$12 - x$。
由題意得：$\frac{4}{7}[10x + (12 - x)] = 10(12 - x) + x$
化簡方程左邊：$\frac{4}{7}(9x + 12)$
方程右邊：$120 - 10x + x = 120 - 9x$
即：$\frac{4}{7}(9x + 12) = 120 - 9x$
兩邊同乘7：$4(9x + 12) = 7(120 - 9x)$
展開：$36x + 48 = 840 - 63x$
移項：$36x + 63x = 840 - 48$
合并同類項：$99x = 792$
解得：$x = 8$
則個位數(shù)字為：$12 - x = 12 - 8 = 4$
所以原來的兩位數(shù)是$84$。
答案：84

12. (2025·宿遷模擬)定義:如果一個一元一次方程的一次項系數(shù)與常數(shù)項的差剛好是這個方程的解的 2 倍,則稱這個方程為“妙解方程”.如:方程 $ 3x + 9 = 0 $ 中, $ 3 - 9 = -6 $,方程的解為 $ x = -3 $,則方程 $ 3x + 9 = 0 $ 為“妙解方程”.請根據(jù)上述定義解答:若關(guān)于 $ x $ 的一元一次方程 $ 3(x - a)-2(1 + x)= 0 $ 是“妙解方程”,則 $ a $ 的值為

$-\frac{1}{3}$

答案：$-\frac{1}{3}$ 解析:因為$3(x - a)-2(1 + x)=0$，所以$3x - 3a - 2 - 2x = 0$，所以$x - 3a - 2 = 0$，所以$x = 3a + 2$。因為關(guān)于$x$的一元一次方程$3(x - a)-2(1 + x)=0$是“妙解方程”，所以$1-(-3a - 2)=2(3a + 2)$，所以$a = -\frac{1}{3}$，所以$a$的值為$-\frac{1}{3}$。

解析：

解：$3(x - a)-2(1 + x)=0$
$3x - 3a - 2 - 2x = 0$
$x - 3a - 2 = 0$
解得$x = 3a + 2$
原方程化為$x - (3a + 2)=0$，一次項系數(shù)為$1$，常數(shù)項為$-(3a + 2)$。
因為方程是“妙解方程”，所以$1 - [-(3a + 2)] = 2(3a + 2)$
$1 + 3a + 2 = 6a + 4$
$3a + 3 = 6a + 4$
$-3a = 1$
$a = -\frac{1}{3}$
答案：$-\frac{1}{3}$

13. 解下列方程:
(1) $ 2x - \frac{1}{2}\left[x - \frac{1}{2}(x - 1)\right]=\frac{2}{3}(x - 1) $;
(2) $ \frac{2}{3}\left[\frac{3}{2}(x - 4)-6\right]=2x + 1 $.

答案：（1）原方程化簡得$\frac{13}{12}x=-\frac{5}{12}$，解得$x=-\frac{5}{13}$。（2）去中括號，得$\frac{2}{3}×\frac{3}{2}(x - 4)-\frac{2}{3}×6 = 2x + 1$，整理，得$x - 4 - 4 = 2x + 1$，移項，得$x - 2x = 1 + 4 + 4$，合并同類項，得$-x = 9$，方程兩邊同時除以$-1$，得$x = - 9$。

解析：

(1)解：$2x - \frac{1}{2}\left[x - \frac{1}{2}(x - 1)\right]=\frac{2}{3}(x - 1)$
去小括號，得$2x - \frac{1}{2}\left(x - \frac{1}{2}x + \frac{1}{2}\right)=\frac{2}{3}x - \frac{2}{3}$
$2x - \frac{1}{2}\left(\frac{1}{2}x + \frac{1}{2}\right)=\frac{2}{3}x - \frac{2}{3}$
去中括號，得$2x - \frac{1}{4}x - \frac{1}{4}=\frac{2}{3}x - \frac{2}{3}$
移項，得$2x - \frac{1}{4}x - \frac{2}{3}x=-\frac{2}{3} + \frac{1}{4}$
合并同類項，得$\frac{24}{12}x - \frac{3}{12}x - \frac{8}{12}x=-\frac{8}{12} + \frac{3}{12}$
$\frac{13}{12}x=-\frac{5}{12}$
系數(shù)化為1，得$x=-\frac{5}{13}$
(2)解：$\frac{2}{3}\left[\frac{3}{2}(x - 4)-6\right]=2x + 1$
去中括號，得$\frac{2}{3}×\frac{3}{2}(x - 4)-\frac{2}{3}×6=2x + 1$
$x - 4 - 4=2x + 1$
移項，得$x - 2x=1 + 4 + 4$
合并同類項，得$-x=9$
系數(shù)化為1，得$x=-9$

14. 已知數(shù)軸上 $ A,B $ 兩點對應(yīng)的數(shù)分別為 $ -20 $, 40, $ P $ 為數(shù)軸上一動點,對應(yīng)的數(shù)為 $ x $,若點 $ P $ 到 $ A,B $ 兩點的距離的比為 $ 2:3 $,求 $ x $ 的值.

答案：若點$P$在點$A$左邊，即$x ＜ - 20$時，根據(jù)題意得$3(-20 - x)=2(40 - x)$，解得$x = - 140$；若點$P$在點$A$和點$B$之間，即$-20 ＜ x ＜ 40$時，根據(jù)題意得$3(x + 20)=2(40 - x)$，解得$x = 4$。綜上所述，$x$的值為$-140$或4。

解析：

解：點P到A、B兩點的距離分別為|x - (-20)| = |x + 20|，|x - 40|。
依題意，|x + 20| : |x - 40| = 2 : 3，即3|x + 20| = 2|x - 40|。
當(dāng)x ＜ -20時，x + 20 ＜ 0，x - 40 ＜ 0，
方程化為3(-x - 20) = 2(40 - x)，
-3x - 60 = 80 - 2x，
-x = 140，
解得x = -140。
當(dāng)-20 ≤ x ≤ 40時，x + 20 ≥ 0，x - 40 ≤ 0，
方程化為3(x + 20) = 2(40 - x)，
3x + 60 = 80 - 2x，
5x = 20，
解得x = 4。
當(dāng)x ＞ 40時，x + 20 ＞ 0，x - 40 ＞ 0，
方程化為3(x + 20) = 2(x - 40)，
3x + 60 = 2x - 80，
x = -140（不符合x ＞ 40，舍去）。
綜上所述，x的值為-140或4。

15. 閱讀解題:解方程: $ |2x - 1|-|x - 2|= 9 $.
解:令 $ 2x - 1 = 0 $,解得 $ x = \frac{1}{2} $.令 $ x - 2 = 0 $,解得 $ x = 2 $.
$ \frac{1}{2} $, 2 這兩個數(shù)將數(shù)軸分成三個部分,如圖所示,下面分類討論.

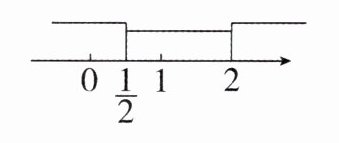
①當(dāng) $ x ＜ \frac{1}{2} $ 時,原方程可變形為 $ -(2x - 1)+(x - 2)= 9 $,
整理得 $ -x - 1 = 9 $,解得 $ x = -10 $.
因為 $ -10 ＜ \frac{1}{2} $,所以方程有解,解為 $ x = -10 $.
②當(dāng) $ \frac{1}{2} \leq x ＜ 2 $ 時,原方程可變形為 $ (2x - 1)+(x - 2)= 9 $,
整理得 $ 3x - 3 = 9 $,解得 $ x = 4 $.
因為 $ 4 ＞ 2 $,所以方程無解.
③當(dāng) $ x \geq 2 $ 時,原方程可變形為 $ (2x - 1)-(x - 2)= 9 $,
整理得 $ x + 1 = 9 $,解得 $ x = 8 $.
因為 $ 8 ＞ 2 $,所以方程有解,解為 $ x = 8 $.
故原方程的解是 $ x = -10 $ 或 $ x = 8 $.
請你模仿上面例題的解法,解方程: $ |x - 3|-3|x + 2|= x - 9 $.

答案：令$x - 3 = 0$，解得$x = 3$。令$x + 2 = 0$，解得$x = - 2$。-2，3這兩個數(shù)將數(shù)軸分成三個部分，如圖所示，下面分類討論。![img alt=15]①當(dāng)$x ＜ - 2$時，原方程可變形為$3 - x - 3(-x - 2)=x - 9$，整理得$3 - x + 3(x + 2)=x - 9$，解得$x = - 18$。因為$-18 ＜ - 2$，所以方程有解，解為$x = - 18$。②當(dāng)$-2\leqslant x ＜ 3$時，原方程可變形為$3 - x - 3(x + 2)=x - 9$，整理得$3 - x - 3x - 6 = x - 9$，解得$x=\frac{6}{5}$。因為$-2 ＜ \frac{6}{5} ＜ 3$，所以方程有解，解為$x=\frac{6}{5}$。③當(dāng)$x\geqslant3$時，原方程可變形為$x - 3 - 3(x + 2)=x - 9$，整理得$x - 3 - 3x - 6 = x - 9$，解得$x = 0$。因為$0 ＜ 3$，所以方程無解。故原方程的解是$x = - 18$或$x=\frac{6}{5}$。

亚洲激情+欧美激情,无码任你躁久久久久久,我的极品美女老婆,性欧美牲交在线视频,亚洲av高清在线一区二区三区