10. (2024·長(zhǎng)春校級(jí)月考)如圖,將一塊長(zhǎng)方形鐵皮的4個(gè)角各剪去一個(gè)邊長(zhǎng)為1m的正方形后,剩下的部分剛好能圍成一個(gè)容積為$15m^3$的無(wú)蓋長(zhǎng)方體盒子,且此盒子底面的長(zhǎng)比寬多2m.設(shè)該長(zhǎng)方體盒子底面的寬為x m.
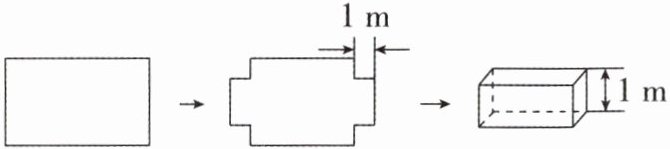
(1)用含x的代數(shù)式分別表示出該長(zhǎng)方體盒子底面的長(zhǎng)和容積;
(2)請(qǐng)根據(jù)題意列出關(guān)于x的方程.
答案:(1)長(zhǎng)方體盒子底面的寬為$x$m,則長(zhǎng)為$(x + 2)$m.容積為$x(x + 2)×1 = x(x + 2)m^{3}$. (2)根據(jù)題意,得$x(x + 2) = 15$.
解析:
(1)長(zhǎng)方體盒子底面的寬為$x\ \text{m}$�,則長(zhǎng)為$(x + 2)\ \text{m}$����。容積為$x(x + 2)×1 = x(x + 2)\ \text{m}^3$�����。
(2)$x(x + 2) = 15$。
11. 小麗在水果店花18元買了蘋果和橘子共6kg,已知蘋果每千克3.2元,橘子每千克2.6元.小麗買了蘋果和橘子各多少千克?
(1)設(shè)所購(gòu)買的蘋果質(zhì)量為x kg.
①根據(jù)“買蘋果的金額+買橘子的金額= 18元”,列方程為
3.2x + 2.6(6 - x) = 18
;
②根據(jù)“所買蘋果的質(zhì)量+所買橘子的質(zhì)量= 6kg”,列方程為
x+\frac{18 - 3.2x}{2.6}=6
;
③根據(jù)“蘋果的單價(jià)×其質(zhì)量= 買蘋果的金額”,列方程為
3.2x = 18 - 2.6(6 - x)
.
(2)設(shè)買蘋果的金額為y元,下列方程正確的是
①③
.(填序號(hào))
①$\frac{y}{3.2} + \frac{18 - y}{2.6} = 6$;
②$y + 2.6(6 - \frac{18 - y}{3.2}) = 18$;
③$3.2(6 - \frac{18 - y}{2.6}) = y$;
④$3.2(6 - \frac{18 - y}{2.6}) = 18 - y$.
答案:(1)①$3.2x + 2.6(6 - x) = 18$ ②$x+\frac{18 - 3.2x}{2.6}=6$③$3.2x = 18 - 2.6(6 - x)$ (2)①③
12. 某校四個(gè)班為“希望工程”捐款,甲班捐的錢數(shù)是另外三個(gè)班捐款總和的一半,乙班捐的錢數(shù)是另外三個(gè)班捐款總和的$\frac{1}{3}$,丙班捐的錢數(shù)是另外三個(gè)班捐款總和的$\frac{1}{4}$,丁班共捐了169元,若設(shè)這四個(gè)班捐款數(shù)的總和為x元,請(qǐng)根據(jù)條件列出方程:
$x-\frac{1}{3}x-\frac{1}{4}x-\frac{1}{5}x = 169$
.
答案:$x-\frac{1}{3}x-\frac{1}{4}x-\frac{1}{5}x = 169$ 解析:因?yàn)榧装嗑璧腻X數(shù)是另外三個(gè)班捐款總和的一半,所以甲班的捐款數(shù)是四個(gè)班捐款數(shù)總和的$\frac{1}{3}$.因?yàn)橐野嗑璧腻X數(shù)是另外三個(gè)班捐款總和的$\frac{1}{3}$,所以乙班的捐款數(shù)是四個(gè)班捐款數(shù)總和的$\frac{1}{4}$.因?yàn)楸嗑璧腻X數(shù)是另外三個(gè)班捐款總和的$\frac{1}{4}$,所以丙班的捐款數(shù)是四個(gè)班捐款數(shù)總和的$\frac{1}{5}$.四個(gè)班捐款數(shù)的總和為$x$元,則甲班捐款$\frac{1}{3}x$元,乙班捐款$\frac{1}{4}x$元,丙班捐款$\frac{1}{5}x$元,根據(jù)題意可列出方程為$x-\frac{1}{3}x-\frac{1}{4}x-\frac{1}{5}x = 169$.
解析:
解:設(shè)這四個(gè)班捐款數(shù)的總和為$x$元���。
因?yàn)榧装嗑璧腻X數(shù)是另外三個(gè)班捐款總和的一半���,所以甲班捐款數(shù)占四個(gè)班總和的$\frac{1}{1 + 2} = \frac{1}{3}$,即甲班捐款$\frac{1}{3}x$元;
因?yàn)橐野嗑璧腻X數(shù)是另外三個(gè)班捐款總和的$\frac{1}{3}$�,所以乙班捐款數(shù)占四個(gè)班總和的$\frac{1}{1 + 3} = \frac{1}{4}$,即乙班捐款$\frac{1}{4}x$元�;
因?yàn)楸嗑璧腻X數(shù)是另外三個(gè)班捐款總和的$\frac{1}{4}$,所以丙班捐款數(shù)占四個(gè)班總和的$\frac{1}{1 + 4} = \frac{1}{5}$���,即丙班捐款$\frac{1}{5}x$元��;
丁班捐款$169$元���,根據(jù)四個(gè)班捐款總和為$x$元,可列方程:$x - \frac{1}{3}x - \frac{1}{4}x - \frac{1}{5}x = 169$��。
$x - \frac{1}{3}x - \frac{1}{4}x - \frac{1}{5}x = 169$
13. 新題型 新定義 方程的解的定義:使方程兩邊相等的未知數(shù)的值.如果一個(gè)方程的解都是整數(shù),那么這個(gè)方程叫作“立信方程”.
(1)若“立信方程”$2x + 1 = 1$的解也是關(guān)于x的方程$1 - 2(x - m) = 3$的解,則$m = $
1
;
(2)若關(guān)于x的方程$x^{2} + 3x - 4 = 0$的解也是“立信方程”$6x + 2x^{2} - 3 - n = 0$的解,求n的值;
5
(3)關(guān)于x的方程$9x - 3 = kx + 14$是“立信方程”,直接寫出符合要求的正整數(shù)k的值.
8,10,26
答案:(1)1 解析:因?yàn)?2x + 1 = 1$,所以$x = 0$,把$x = 0$代入$1 - 2(x - m) = 3$得$1 - 2(0 - m) = 3$,即$1 + 2m = 3$,得$m = 1$. (2)因?yàn)?x^{2}+3x - 4 = 0$,所以$x^{2}+3x = 4$,則$2(x^{2}+3x)=2x^{2}+6x = 8$.將$2x^{2}+6x = 8$代入$6x + 2x^{2}-3 - n = 0$,得$8 - 3 - n = 0$,得$n = 5$. (3)符合要求的正整數(shù)$k$的值為8,10,26. 解析:由$9x - 3 = kx + 14$得$x=\frac{17}{9 - k}(k\neq9)$,當(dāng)$9 - k$取$1,-1,17,-17$,即$k$取8,10,-8,26時(shí),$x$的值為整數(shù).所以符合要求的正整數(shù)$k$的值為8,10,26.
解析:
(1)解:解方程$2x + 1 = 1$��,得$2x=0$�,$x = 0$。
把$x = 0$代入$1 - 2(x - m) = 3$�����,得$1 - 2(0 - m)=3$�,即$1 + 2m = 3$,$2m=2$�,$m = 1$。
(2)解:解方程$x^{2}+3x - 4 = 0$,因式分解得$(x + 4)(x - 1)=0$����,$x + 4 = 0$或$x - 1 = 0$,解得$x=-4$或$x = 1$��。
由$x^{2}+3x - 4 = 0$得$x^{2}+3x=4$�����,則$2x^{2}+6x=8$��。
將$2x^{2}+6x = 8$代入$6x + 2x^{2}-3 - n = 0$�����,得$8 - 3 - n = 0$���,$5 - n = 0$,$n = 5$�。
(3)8,10��,26