11. 新題型 新運(yùn)算 (2024·瀘州模擬)從n個(gè)不同元素中取出m個(gè)元素的所有不同組合的個(gè)數(shù),叫作從n個(gè)不同元素中取出m個(gè)元素的組合數(shù),用符號(hào)$C_{n}^{m}$表示.已知“!”是一種數(shù)學(xué)運(yùn)算符號(hào),且$1!= 1,2!= 2×1= 2,3!= 3×2×1= 6,4!= 4×3×2×1= 24,... $,若公式$C_{n}^{m}= \frac {n!}{m!(n-m)!}(n≥m,m,n$為正整數(shù)),則$C_{7}^{5}$為_(kāi)___
21
.
答案:21 解析:因?yàn)?C_{n}^{m}=\frac{n!}{m!(n-m)!}(n≥m$,n,m為正整數(shù)),所以$C_{7}^{5}=\frac{7!}{5!(7-5)!}=\frac{7×6×5×4×3×2×1}{5×4×3×2×1×2×1}=21$.
解析:
解:$C_{7}^{5}=\frac{7!}{5!(7-5)!}=\frac{7×6×5×4×3×2×1}{(5×4×3×2×1)×(2×1)}=\frac{5040}{120×2}=21$
答案:21
12. 計(jì)算:
(1)$[-2^{4}÷(-2\frac {2}{3})^{2}-\frac {11}{2}]÷\frac {1}{12};$
(2)$|-\frac {5}{7}|×(\frac {4}{5}-\frac {1}{3})÷(-\frac {2}{3})^{2}-(\frac {1}{2})^{2}.$
答案:(1)-93 (2)$\frac{1}{2}$
解析:
(1)解:原式$=[-16÷ \left(-\frac{8}{3}\right)^2-\frac{11}{2}]÷ \frac{1}{12}$
$=[-16÷ \frac{64}{9}-\frac{11}{2}]× 12$
$=[-16× \frac{9}{64}-\frac{11}{2}]× 12$
$=[-\frac{9}{4}-\frac{22}{4}]× 12$
$=(-\frac{31}{4})× 12$
$=-93$
(2)解:原式$=\frac{5}{7}× (\frac{12}{15}-\frac{5}{15})÷ \frac{4}{9}-\frac{1}{4}$
$=\frac{5}{7}× \frac{7}{15}× \frac{9}{4}-\frac{1}{4}$
$=\frac{1}{3}× \frac{9}{4}-\frac{1}{4}$
$=\frac{3}{4}-\frac{1}{4}$
$=\frac{1}{2}$
13. 有個(gè)寫(xiě)運(yùn)算符號(hào)的游戲:在“$3□ (2□ 3)□ \frac {4}{3}□ 2^{2}$”中的每個(gè)$□$內(nèi)填入“+”“-”“×”“÷”中的某一個(gè)(可重復(fù)使用),然后計(jì)算結(jié)果.
(1)請(qǐng)計(jì)算琪琪填入符號(hào)后得到的算式:$3×(2÷3)-\frac {4}{3}÷2^{2};$
$\frac{5}{3}$
(2)嘉嘉填入符號(hào)后得到的算式是$3÷(2×3)×\frac {4}{3}□ 2^{2}$,一不小心擦掉了$□$里的運(yùn)算符號(hào),但她知道結(jié)果是$-\frac {10}{3}$,請(qǐng)推算出$□$內(nèi)的符號(hào).
-
答案:(1)$3×(2÷3)-\frac{4}{3}÷2^{2}=3×(2÷3)-\frac{4}{3}×\frac{1}{4}=3×\frac{2}{3}-\frac{1}{3}=2-\frac{1}{3}=\frac{5}{3}$.(2)$3÷(2×3)×\frac{4}{3}□2^{2}=3÷6×\frac{4}{3}□2^{2}=\frac{2}{3}□4=-\frac{10}{3}$.因?yàn)?\frac{2}{3}-4=-\frac{10}{3}$,所以□里的符號(hào)應(yīng)是“-”.
解析:
(1)解:$3×(2÷3)-\frac{4}{3}÷2^{2}$
$=3×\frac{2}{3}-\frac{4}{3}÷4$
$=2-\frac{4}{3}×\frac{1}{4}$
$=2-\frac{1}{3}$
$=\frac{5}{3}$
(2)解:$3÷(2×3)×\frac{4}{3}□2^{2}$
$=3÷6×\frac{4}{3}□4$
$=\frac{1}{2}×\frac{4}{3}□4$
$=\frac{2}{3}□4$
因?yàn)榻Y(jié)果是$-\frac{10}{3}$����,且$\frac{2}{3}-4=-\frac{10}{3}$��,所以$□$內(nèi)的符號(hào)是“$-$”�����。
14. 新考法 (2025·南通校級(jí)月考)取一個(gè)自然數(shù),若它是奇數(shù),則加上1,若它是偶數(shù),則除以2,按此規(guī)則經(jīng)過(guò)若干步的計(jì)算最終可得到1(注:計(jì)算到1結(jié)束).這個(gè)結(jié)論在數(shù)學(xué)上還沒(méi)有得到證明,但舉例驗(yàn)證都是正確的.例如,取自然數(shù)5,經(jīng)過(guò)下面5步運(yùn)算可得1,如圖所示.如果自然數(shù)m恰好經(jīng)過(guò)5步運(yùn)算可得到1,那么所有符合條件的m的值有 (
C
)
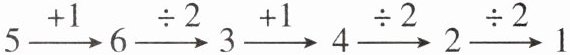
A.3個(gè)
B.4個(gè)
C.5個(gè)
D.6個(gè)
答案:C 解析:設(shè)自然數(shù)m為第一個(gè)數(shù),經(jīng)過(guò)1步運(yùn)算得到的數(shù)為第二個(gè)數(shù),以此類(lèi)推,經(jīng)過(guò)5步運(yùn)算得到的1為第六個(gè)數(shù),則第五個(gè)數(shù)為$1×2=2$,第四個(gè)數(shù)為$2×2=4$.①若第三個(gè)數(shù)是奇數(shù),則第三個(gè)數(shù)為$4-1=3$,所以第二個(gè)數(shù)為$3×2=6$,所以第一個(gè)數(shù)$m=6-1=5$或$m=6×2=12$;②若第三個(gè)數(shù)是偶數(shù),則第三個(gè)數(shù)為$4×2=8$,所以第二個(gè)數(shù)為$8×2=16$或$8-1=7$,所以第一個(gè)數(shù)$m=16-1=15$或$m=16×2=32$或$m=7×2=14$.綜上,所有符合條件的m的值為5,12,14,15,32,共有5個(gè).故選C.
15. 觀察下列各式:
$1^{3}= 1= \frac {1}{4}×1^{2}×2^{2};$
$1^{3}+2^{3}= 9= \frac {1}{4}×2^{2}×3^{2};$
$1^{3}+2^{3}+3^{3}= 36= \frac {1}{4}×3^{2}×4^{2};$
$1^{3}+2^{3}+3^{3}+4^{3}= 100= \frac {1}{4}×4^{2}×5^{2};$
…
回答下面的問(wèn)題:
(1)$1^{3}+2^{3}+3^{3}+4^{3}+5^{3}=$____
$\frac{1}{4}×5^{2}×6^{2}$
;
(2)計(jì)算$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}$的值;
$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}=\frac{1}{4}×100^{2}×101^{2}=25502500$
(3)計(jì)算$11^{3}+12^{3}+... +99^{3}+100^{3}$的值.
原式$=\frac{1}{4}×100^{2}×101^{2}-\frac{1}{4}×10^{2}×11^{2}=25502500-3025=25499475$
答案:(1)$\frac{1}{4}×5^{2}×6^{2}$(2)$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}=\frac{1}{4}×100^{2}×101^{2}=25502500$.(3)原式$=\frac{1}{4}×100^{2}×101^{2}-\frac{1}{4}×10^{2}×11^{2}=25502500-3025=25499475$.
解析:
(1)$\frac{1}{4}×5^{2}×6^{2}$
(2)解:$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}$
$=\frac{1}{4}×100^{2}×101^{2}$
$=\frac{1}{4}×10000×10201$
$=2500×10201$
$=25502500$
(3)解:$11^{3}+12^{3}+... +99^{3}+100^{3}$
$=(1^{3}+2^{3}+... +99^{3}+100^{3})-(1^{3}+2^{3}+... +10^{3})$
$=\frac{1}{4}×100^{2}×101^{2}-\frac{1}{4}×10^{2}×11^{2}$
$=25502500-\frac{1}{4}×100×121$
$=25502500-25×121$
$=25502500-3025$
$=25499475$