亚洲激情+欧美激情,无码任你躁久久久久久,我的极品美女老婆,性欧美牲交在线视频,亚洲av高清在线一区二区三区

11. 平方等于它本身的數(shù)是,立方等于它本身的數(shù)是,平方等于它相反數(shù)的數(shù)是,立方等于它相反數(shù)的數(shù)是.

12. 觀察下列算式: (1) $3^1= 3$, (2) $3^2= 9$, (3) $3^3= 27$, (4) $3^4= 81$, (5) $3^5= 243$, (6) $3^6= 729$, (7) $3^7= $ 2187 , (8) $3^8= 6561, …$. 根據(jù)算式中的規(guī)律, 你認(rèn)為 $3^{100}$ 的個(gè)位數(shù)字是____.

13. 新題型 新定義 (2024·內(nèi)江校級(jí)月考) 定義:如果$a^x= N(a＞0$, 且$a \neq 1)$, 那么 $x$ 叫作以 $a$ 為底 $N$ 的對(duì)數(shù), 記作 $x= \log _a N$. 例如: 因?yàn)?$7^2= 49$, 所以 $\log _7 49= 2$; 因?yàn)?$5^3= 125$, 所以 $\log _5 125= 3$. 下列說(shuō)法: (1) $\log _6 6= 36$; (2) $\log _3 81= $ 4; (3)若 $\log _4(a+14)= 2$, 則 $a= 2$; (4) $\log _2 64= $ $\log _2 32+\log _2 2$. 正確的有____(填序號(hào)).

14. 閱讀下列各式: $(a × b)^2= a^2 × b^2,(a × b)^3= a^3 ×$ $b^3,(a × b)^4= a^4 × b^4,(a × b)^5= a^5 × b^5 … …$
回答下列問(wèn)題:
(1) 猜想: $(a × b)^n= $.
(2) 請(qǐng)用我們學(xué)過(guò)的知識(shí)說(shuō)明上式成立的理由.

(3) 請(qǐng)計(jì)算:
(1) $\left(-\frac{1}{4}\right)^{1000} × 4^{1000}$;

(2) $(-0.125)^{2025} × 2^{2024} × 4^{2023}$.

15. (2025·深圳期中) 在一次綜合實(shí)踐活動(dòng)課上, 張老師給每位同學(xué)各發(fā)了一張正方形紙片, 請(qǐng)同學(xué)們思考如何通過(guò)折紙的方法求出 $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^6}$ 的值.
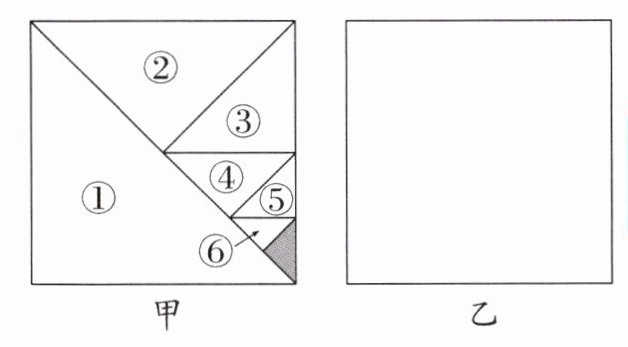
【操作探究】“乘風(fēng)”小組的同學(xué)經(jīng)過(guò)一番思考和討論交流后, 進(jìn)行了如下操作: 如圖甲, 將一個(gè)邊長(zhǎng)為 1 的正方形紙片分割成 7 個(gè)部分, 第(1)部分是邊長(zhǎng)為 1 的正方形紙片面積的一半, 第(2)部分是第(1)部分面積的一半, 第(3)部分是第(2)部分面積的一半……依次類(lèi)推, 則圖甲中空白部分的面積為 $\frac{1}{2}+\frac{1}{4}+$ $\frac{1}{8}+…+\frac{1}{2^6}$.
“破浪”小組是這樣思考的: 設(shè) $S= \frac{1}{2}+\frac{1}{4}+$ $\frac{1}{8}+…+\frac{1}{2^6}$,
將等式兩邊同時(shí)乘 $\frac{1}{2}$ 得 $\frac{1}{2} S= \frac{1}{4}+\frac{1}{8}+…+$ $\frac{1}{2^6}+\frac{1}{2^7}$,
將上式減去下式得 $\frac{1}{2} S= \frac{1}{2}-\frac{1}{2^7}$, 即 $S= 1-\frac{1}{2^6}= $ $\frac{63}{64}$, 即 $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^6}= \frac{63}{64}$.
甲
乙

【過(guò)程思考】
(1) 圖甲中陰影部分的面積是____, $\frac{1}{2}+$ $\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^7}= $____.
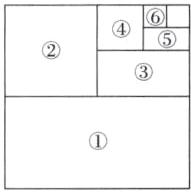
(2) 請(qǐng)你利用圖乙, 再設(shè)計(jì)能求 $\frac{1}{2}+\frac{1}{4}+$ $\frac{1}{8}+…+\frac{1}{2^6}$ 的值的幾何圖形. (只畫(huà)出圖形即可)
(3) 根據(jù)以上規(guī)律, 計(jì)算:
(1) $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^n}= $____; ( $n$ 為正整數(shù))
(2) $2+4+8+16+…+2^n= $____. ( $n$ 為正整數(shù))