1.「2025云南昆明尋甸月考」下列關(guān)于x的方程一定有兩個(gè)實(shí)數(shù)根的是 (
D
)
A. $k^{2}x^{2}-4x-4= 0$
B. $x^{2}-4x+5= 0$
C. $x^{2}-4x+k= 0$
D. $(k^{2}+1)x^{2}= 0$
答案:D A. 當(dāng)$k=0$時(shí)�����,原方程為$-4x - 4 = 0$,有實(shí)數(shù)根$x = -1$�����;當(dāng)$k \neq 0$時(shí)���,$\Delta = 16 + 16k^{2} > 0$�,一元二次方程有兩個(gè)不相等的實(shí)數(shù)根���,故原方程不一定有兩個(gè)實(shí)數(shù)根��,不符合題意���。B. $\Delta = 16 - 4 \times 5 = -4 < 0$,沒有實(shí)數(shù)根���,不符合題意�����。C. $\Delta = 16 - 4k$�����,當(dāng)$16 - 4k < 0$時(shí)�����,沒有實(shí)數(shù)根����,不符合題意��。D. $\Delta = 0$,有兩個(gè)相等的實(shí)數(shù)根���,符合題意���。故選D。
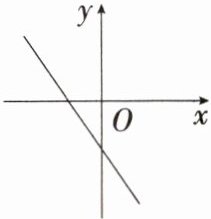
2.「2025河北石家莊期中」在平面直角坐標(biāo)系中,若一次函數(shù)$y= -2x+m$的圖象如圖所示,則關(guān)于x的方程$mx^{2}+x+2= 0$的根的情況是 (
A
)
A.有兩個(gè)不相等的實(shí)數(shù)根
B.有兩個(gè)相等的實(shí)數(shù)根
C.只有一個(gè)實(shí)數(shù)根
D.沒有實(shí)數(shù)根
答案:A 由題中圖象可得$m < 0$���,$\because mx^{2} + x + 2 = 0$���,$\therefore \Delta = 1^{2} - 4m \times 2 = 1 - 8m > 0$,$\therefore$方程$mx^{2} + x + 2 = 0$有兩個(gè)不相等的實(shí)數(shù)根�����。故選A�����。
3.「2024甘肅蘭州中考」關(guān)于x的一元二次方程$9x^{2}-6x+c= 0$有兩個(gè)相等的實(shí)數(shù)根,則$c= $ (
D
)
A.-9
B.4
C.-1
D.1
答案:D $\because$關(guān)于$x$的一元二次方程$9x^{2} - 6x + c = 0$有兩個(gè)相等的實(shí)數(shù)根�,$\therefore \Delta = (-6)^{2} - 4 \times 9 \times c = 0$,解得$c = 1$��。故選D�。
4.「2024黑龍江龍東地區(qū)中考」關(guān)于x的一元二次方程$(m-2)x^{2}+4x+2= 0$有兩個(gè)實(shí)數(shù)根,則m的取值范圍是 (
D
)
A. $m≤4$
B. $m≥4$
C. $m≥-4且m≠2$
D. $m≤4且m≠2$
答案:D 根據(jù)題意�,得$\begin{cases}16 - 4(m - 2) \times 2 \geq 0, \\ m - 2 \neq 0,\end{cases}$解得$m \leq 4$且$m \neq 2$��。故選D���。
5.若恰好只有一個(gè)實(shí)數(shù)a是方程$(k^{2}-9)x^{2}-2(k+1)x+1= 0$的根,則k的值為
±3或-5
.
答案:答案 $\pm 3$或$-5$
解析 ①當(dāng)原方程是一元一次方程時(shí)��,方程只有一個(gè)實(shí)數(shù)根���,則$k^{2} - 9 = 0$���,解得$k = \pm 3$�,此時(shí)$-2(k + 1) \neq 0$����,滿足條件;
②當(dāng)原方程是一元二次方程時(shí)���,方程有兩個(gè)相等的實(shí)數(shù)根�����,則$\Delta = b^{2} - 4ac = 0$����,
即$4(k + 1)^{2} - 4(k^{2} - 9) = 0$,解得$k = -5$��。
綜上�����,$k$的值為$\pm 3$或$-5$�����。
6.「2025江西新余渝水月考」已知關(guān)于x的一元二次方程$x^{2}-5x+6-p^{2}= 0$,求證:無論p取何值,方程總有兩個(gè)不相等的實(shí)數(shù)根.
答案:證明 $\because x^{2} - 5x + 6 - p^{2} = 0$�����,$\therefore a = 1$�����,$b = -5$�,$c = 6 - p^{2}$,
$\therefore \Delta = b^{2} - 4ac = (-5)^{2} - 4(6 - p^{2}) = 25 - 24 + 4p^{2} = 4p^{2} + 1$��,
$\because p^{2} \geq 0$��,$\therefore 4p^{2} + 1 \geq 1$,$\therefore \Delta > 0$�,
$\therefore$方程總有兩個(gè)不相等的實(shí)數(shù)根。
7.「2025江蘇連云港灌云期中」關(guān)于x的方程$2x^{2}+(m+2)x+m= 0$.
(1)求證:無論m取何值,方程總有兩個(gè)實(shí)數(shù)根.
(2)請(qǐng)取一個(gè)合適的m值,并求此時(shí)方程的根.
答案:解析 (1) 證明:$\because 2x^{2} + (m + 2)x + m = 0$�����,
$\therefore a = 2$���,$b = m + 2$����,$c = m$���,
$\therefore \Delta = b^{2} - 4ac = (m + 2)^{2} - 8m = (m - 2)^{2} \geq 0$,
$\therefore$無論$m$取何值�����,方程總有兩個(gè)實(shí)數(shù)根���。
(2) (答案不唯一) 取$m = -2$�,則方程變?yōu)?2x^{2} - 2 = 0$�,解得$x_{1} = 1$�,$x_{2} = -1$�����,
$\therefore$當(dāng)$m = -2$時(shí)����,方程的兩根為$x_{1} = 1$,$x_{2} = -1$����。
8.「2025山東青島嶗山月考」已知$x_{1},x_{2}$是關(guān)于x的方程$x^{2}-2(m+1)x+m^{2}+5= 0$的兩個(gè)實(shí)數(shù)根,等腰$\triangle ABC$的一邊長(zhǎng)為7,若$x_{1},x_{2}恰好是\triangle ABC$另外兩邊長(zhǎng),則$\triangle ABC$的周長(zhǎng)為 (
B
)
A.13
B.17
C.29
D.17或29
答案:B 若等腰$\triangle ABC$的底邊長(zhǎng)為7,則$\Delta = [-2(m + 1)]^{2} - 4(m^{2} + 5) = 8m - 16 = 0$�����,解得$m = 2$�,$\therefore$原方程為$x^{2} - 6x + 9 = 0$,解得$x_{1} = x_{2} = 3$�,$\because 3 + 3 = 6 < 7$,$\therefore$舍去���。若等腰$\triangle ABC$的腰長(zhǎng)為7�,把$x = 7$代入方程$x^{2} - 2(m + 1)x + m^{2} + 5 = 0$�,得$49 - 14(m + 1) + m^{2} + 5 = 0$����,解得$m_{1} = 4$�����,$m_{2} = 10$����,若$m = 4$��,則原方程為$x^{2} - 10x + 21 = 0$����,解得$x_{1} = 7$���,$x_{2} = 3$����,$\because 3 + 7 = 10 > 7$��,$\therefore$符合題意��;若$m = 10$�����,則原方程為$x^{2} - 22x + 105 = 0$��,解得$x_{1} = 7$���,$x_{2} = 15$,$\because 7 + 7 = 14 < 15$���,$\therefore$舍去���。綜上����,滿足條件的$\triangle ABC$的周長(zhǎng)為$7 + 7 + 3 = 17$,故選B���。
9.已知關(guān)于x的一元二次方程$(a+c)x^{2}+2bx+(c-a)= 0$,其中2a,2b分別為$//ogram ABCD$的對(duì)角線AC,BD的長(zhǎng),c為邊AB的長(zhǎng).
(1)如果方程有兩個(gè)相等的實(shí)數(shù)根,試判斷四邊形ABCD的形狀,并說明理由.
(2)如果四邊形ABCD為正方形,試求這個(gè)一元二次方程的根.
答案:解析 (1) 四邊形$ABCD$是菱形�。理由如下:
$\because$一元二次方程$(a + c)x^{2} + 2bx + (c - a) = 0$有兩個(gè)相等的實(shí)數(shù)根���,$\therefore (2b)^{2} - 4(a + c)(c - a) = 0$,
化簡(jiǎn),得$a^{2} + b^{2} = c^{2}$���。
$\because 2a$,$2b$分別為$\square ABCD$的對(duì)角線$AC$,$BD$的長(zhǎng)�,$c$為邊$AB$的長(zhǎng),$\therefore \square ABCD$的對(duì)角線$AC$�,$BD$互相垂直。
$\therefore$四邊形$ABCD$是菱形。
(2) $\because$四邊形$ABCD$為正方形��,$2a$����,$2b$分別為$\square ABCD$的對(duì)角線$AC$���,$BD$的長(zhǎng)����,$c$為邊$AB$的長(zhǎng),
$\therefore a^{2} + b^{2} = c^{2}$�,$a = b = \frac{\sqrt{2}}{2}c$��,$c = \sqrt{2}b$���。
$\therefore \Delta = (2b)^{2} - 4(a + c)(c - a) = 4(b^{2} + a^{2} - c^{2}) = 0$��。
$\therefore x = \frac{-2b}{2(a + c)} = \frac{-b}{b + \sqrt{2}b} = 1 - \sqrt{2}$��。
即這個(gè)一元二次方程的根是$x_{1} = x_{2} = 1 - \sqrt{2}$���。