20.「2024 江蘇宿遷中考」(6 分)某校組織七年級(jí)學(xué)生開展以“講好紅色故事,傳承紅色基因”為主題的研學(xué)活動(dòng),策劃了四條研學(xué)線路供學(xué)生選擇:A.彭雪楓紀(jì)念館,B.淮海軍政大禮堂,C.愛園烈士陵園,D.大王莊黨性教育基地,每名學(xué)生只能任意選擇一條線路.
(1)小剛選擇線路 A 的概率為
$\frac{1}{4}$
.
(2)請(qǐng)用畫樹狀圖或列表的方法,求小剛和小紅選擇同一線路的概率.
小紅小剛
A B C D A (A,A) (A,B) (A,C) (A,D) B (B,A) (B,B) (B,C) (B,D) C (C,A) (C,B) (C,C) (C,D) D (D,A) (D,B) (D,C) (D,D)共有16種等可能的結(jié)果,其中小剛和小紅選擇同一線路的結(jié)果有4種,$\therefore $小剛和小紅選擇同一線路的概率為
$\frac{1}{4}$
.
答案:20. 解析 (1)$\frac {1}{4}$. …………………………… (2分)(2)列表如下:____ A B C D A (A,A) (A,B) (A,C) (A,D) B (B,A) (B,B) (B,C) (B,D) C (C,A) (C,B) (C,C) (C,D) D (D,A) (D,B) (D,C) (D,D)共有16種等可能的結(jié)果,其中小剛和小紅選擇同一線路的結(jié)果有4種,$\therefore $小剛和小紅選擇同一線路的概率為$\frac {4}{16}=\frac {1}{4}$. …… (6分)
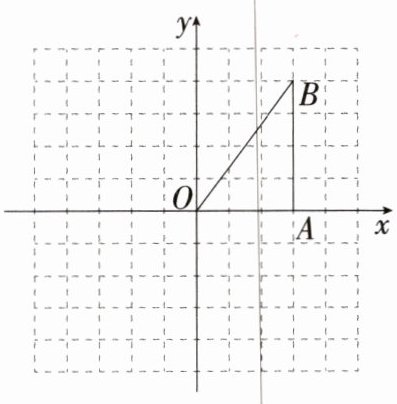
21.(8 分)如圖所示的方格紙(1 格長(zhǎng)為一個(gè)單位長(zhǎng)度)中,$ \triangle AOB $ 的頂點(diǎn)坐標(biāo)分別為 $ A(3,0),O(0,0),B(3,4) $.
(1)將 $ \triangle AOB $ 沿 $ x $ 軸向左平移 5 個(gè)單位,畫出平移后的 $ \triangle A_1O_1B_1 $(不寫作法,但要標(biāo)出頂點(diǎn)字母).
(2)將 $ \triangle AOB $ 繞點(diǎn) $ O $ 順時(shí)針旋轉(zhuǎn) $ 90^\circ $,畫出旋轉(zhuǎn)后的 $ \triangle A_2O_2B_2 $(不寫作法,但要標(biāo)出頂點(diǎn)字母).
(3)在(2)的條件下,求點(diǎn) $ B $ 繞點(diǎn) $ O $ 旋轉(zhuǎn)到點(diǎn) $ B_2 $ 所經(jīng)過的路徑長(zhǎng)(結(jié)果保留 $ \pi $).
答案:21. 解析 (1)如圖,$△A_{1}O_{1}B_{1}$即為所求.

……………………………… (2分)(2)如圖,$△A_{2}O_{2}B_{2}$即為所求. ……………… (4分)(3)由圖可知,點(diǎn)B繞點(diǎn)O旋轉(zhuǎn)到點(diǎn)$B_{2}$所經(jīng)過的路徑是弧$BB_{2}$,在$Rt△AOB$中,$OB=\sqrt {OA^{2}+AB^{2}}=5,\therefore $路徑長(zhǎng)$=\frac {90}{360}×2π×5=\frac {5}{2}π$. ……………… (8分)
22.「2023 湖南郴州中考」(8 分)如圖,在 $ \odot O $ 中,$ AB $ 是直徑,點(diǎn) $ C $ 是圓上一點(diǎn).在 $ AB $ 的延長(zhǎng)線上取一點(diǎn) $ D $,連接 $ CD $,使 $ \angle BCD = \angle A $.
(1)求證:直線 $ CD $ 是 $ \odot O $ 的切線.
(2)若 $ \angle ACD = 120^\circ,CD = 2\sqrt{3} $,求圖中陰影部分的面積(結(jié)果用含 $ \pi $ 的式子表示).

答案:22. 解析 (1)證明:連接OC,

$\because AB$是直徑,$\therefore ∠ACB=∠OCA+∠OCB=90^{\circ }$. …………… (2分)$\because OA=OC,∠BCD=∠A,\therefore ∠OCA=∠A=∠BCD,\therefore ∠BCD+∠OCB=∠OCD=90^{\circ },\therefore OC⊥CD$. ………………………………… (3分)$\because OC$是$\odot O$的半徑,$\therefore $直線CD是$\odot O$的切線. ………………… (4分)(2)$\because ∠ACD=120^{\circ },∠ACB=90^{\circ },\therefore ∠A=∠BCD=120^{\circ }-90^{\circ }=30^{\circ },\therefore ∠BOC=2∠A=60^{\circ }$, ……………………… (5分)$\therefore ∠D=90^{\circ }-∠BOC=90^{\circ }-60^{\circ }=30^{\circ },\therefore OD=2OC$,在$Rt△OCD$中,$OC^{2}+CD^{2}=OD^{2}$,即$OC^{2}+(2\sqrt {3})^{2}=4OC^{2}$,解得$OC = 2$(舍負(fù)), ………………………… (6分)$\therefore S_{陰影部分}=S_{\triangle OCD}-S_{扇形BOC}=\frac {1}{2}×2\sqrt {3}×2-\frac {60×π×2^{2}}{360}=2\sqrt {3}-\frac {2π}{3}$. ………………………………… (8分)
23.「2025 山東濱州鄒平一?!?10 分)某水果批發(fā)商銷售每箱進(jìn)價(jià)為 40 元的蘋果,物價(jià)部門規(guī)定每箱銷售價(jià)不得高于 72 元,市場(chǎng)調(diào)查發(fā)現(xiàn),若每箱以 50 元的價(jià)格銷售,平均每天銷售 500 箱,每箱價(jià)格每提高 1 元平均每天少銷售 10 箱.設(shè)每箱漲價(jià) $ x $ 元,每天盈利 $ y $ 元.
(1)列出 $ y $ 與 $ x $ 的函數(shù)關(guān)系式.
(2)若該批發(fā)商要盈利 8750 元,則每箱蘋果的售價(jià)為多少元?
(3)當(dāng)每箱蘋果的售價(jià)為多少元時(shí),可獲得最大利潤? 最大利潤是多少?
答案:23. 解析 (1)由題意得$y=(x + 50 - 40)(500 - 10x)$,化簡(jiǎn)得$y=-10x^{2}+400x + 5000$. …………… (2分)(2)由題意可得$8750=-10x^{2}+400x + 5000$,化簡(jiǎn)得$(x - 25)(x - 15)=0$,解得$x_{1}=25,x_{2}=15,\because 50 + 25 = 75>72,50 + 15 = 65<72,\therefore $每箱蘋果的售價(jià)為65元. ………………… (5分)(3)$y=-10x^{2}+400x + 5000=-10(x^{2}-40x + 400 - 400)+5000=-10(x - 20)^{2}+9000,\because -10<0,\therefore $當(dāng)$x = 20$時(shí),y有最大值,最大值為9000,$\therefore $當(dāng)每箱蘋果的售價(jià)為$50 + 20 = 70$元時(shí),可獲得最大利潤,最大利潤是9000元. …………… (10分)