?$OE\perp CD$?�����,理由如下:
證明:延長?$OE$?至點(diǎn)?$GF$?,使得?$EG = OE$?�����,
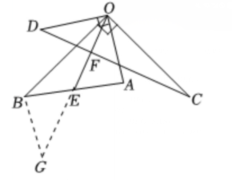
?$∵E$?是?$AB$?的中點(diǎn)����,
?$∴AE = BE$?,
在?$\triangle AEO$?和?$\triangle BEG$?中�,
?$\{\begin {array}{l}AE = BE\\∠AEO=∠BEG\\OE = EG\end {array}.$?
?$∴\triangle AEO\cong \triangle BEG(\mathrm {SAS})$?,
?$∴BG = AO = OD$?��,?$∠A=∠GBE$?��,
?$∴BG// AO$?����,
?$∴∠GBO+∠AOB = 180°$?,
又?$OA\perp OD$?����,?$OB\perp OC$?,
?$∴∠DOC = 180°-∠AOB$?�,即?$∠DOC+∠AOB = 180°$?,
?$∴∠GBO=∠DOC$?,
在?$\triangle GBO$?和?$\triangle ODC$?中���,
?$\{\begin {array}{l}BG = OD\\∠GBO=∠DOC\\OB = OC\end {array}.$?
?$∴\triangle GBO\cong \triangle ODC(\mathrm {SAS})$?����,
?$∴∠BOG=∠OCD$?����,
又?$∠BOG+∠FOC = 90°$?,
?$∴∠OCD+∠FOC = 90°$?�,
?$∴∠OFC = 90°$?,即?$OE\perp CD$?���;