解:?$(1)$?∵在?$\odot O$?中�,?$AB$?是?$\odot O$?的弦
∴?$OA=OB$?
∵?$∠AOB=60°����,$??$AB=2$?
∴?$△OAB$?是等邊三角形,?$OA=OB=AB=2$?
過(guò)點(diǎn)?$O$?作?$OC⊥AB��,$?垂足為?$C�,$?如圖
則?$AC=\frac 12AB=\frac 12×2=1$?
在?$Rt△OAC$?中,?$∠OCA=90°����,$??$OA=2,$??$AC=1$?
根據(jù)勾股定理���,得?$OC=\sqrt {OA^2-AC^2}=\sqrt {2^2-1^2}=\sqrt {3}$?
∴?$S_{△OAB}=\frac 12AB ·OC=\frac 12×2×\sqrt {3}=\sqrt {3}$?
又∵?$∠AOB=60°��,$??$△OAB$?是等邊三角形且邊長(zhǎng)是?$2$?
∴?$S_{扇形OAB}=\frac {60}{360}×π×2^2=\frac 23π$?
又∵點(diǎn)?$P $?到直線?$AB$?的距離為?$x�����,$??$AB=2$?
∴?$S_{△PAB}=\frac 12\ \mathrm {·}x=\frac 12×2×x=x$?
∴圖中的陰影部分的面積?$y=S_{△PAB}+S_{扇形OAB}-S_{△OAB}=x+\frac 23π-\sqrt {3}$?
自變量?$x$?的取值范圍是?$0<x≤2+\sqrt {3}$?
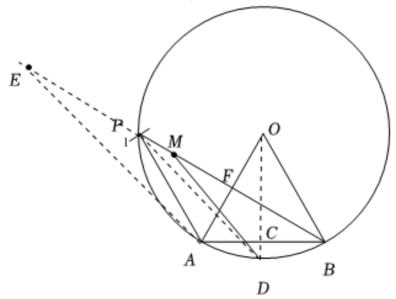
?$(2)①$?如圖所示����,分別以點(diǎn)?$A($?或點(diǎn)?$B)$?為圓心��,以?$AB$?的長(zhǎng)為半徑畫(huà)弧交?$\odot O$?
于點(diǎn)?$P_{1}($?或?$P_{2})$?
②折線的畫(huà)法�,以過(guò)點(diǎn)?$P_{1}$?的情況為例
過(guò)點(diǎn)?$O$?作?$OC⊥AB,$?垂足為?$C�,$?延長(zhǎng)?$OC$?交?$\odot O$?于點(diǎn)?$D$?
連接?$P_{1}C、$??$CD�����,$?則折線?$P_{1}-C-D$?即為所求
弧線的畫(huà)法����,以點(diǎn)?$P_{1}$?的情況為例
以?$P_{1}$?為圓心,?$P_{1}A$?長(zhǎng)為半徑畫(huà)弧����,交?$P_{1}B$?于點(diǎn)?$F,$?則?$\widehat {AF}$?即為作求
直線的畫(huà)法�����,以點(diǎn)?$P_{1}$?的情況為例
作?$OC⊥AB���,$??$C$?為垂足��,延長(zhǎng)?$OC$?交?$\odot O$?于點(diǎn)?$D$?
連接?$P_{1}D��,$?過(guò)點(diǎn)?$A$?作?$AE//P_{1}D�����,$?交?$BP_{1}$?延長(zhǎng)線于點(diǎn)?$E$?
取?$BE$?的中點(diǎn)?$M����,$?則線段?$DM$?即為所求
答:不寫(xiě)作法。