解?$: (1)$?過?$O$?點作?$OE⊥AB �����,$?交圓?$O$?于?$D �����,$?連接?$AO$
?
∴?$ AE= BE=\frac 12AB=4,$??$OE= 3$?
在?$Rt△AHE$?中���,?$AO= \sqrt {AE^2+OE^2} =5$?
?$(2)$?如圖:?$OD=OA=OB=5�����,$??$OE⊥AB�,$??$ OE= 3$?
∴?$DE=OD -OE=5-3 =2\ \mathrm {cm}$?
∴點?$D$?是圓上到?$AB$?距離為?$2\ \mathrm {cm} $?的點
∵?$OE = 3\ \mathrm {cm} >2\ \mathrm {cm}$?
∴在?$OD$?上截取?$OH = 1\ \mathrm {cm}$?
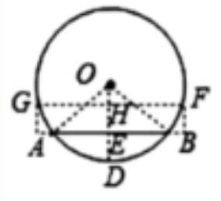
過點?$H$?作?$GF//AB ����,$?交圓于點?$G ,$??$ F $?兩點�,
則有?$HE⊥ AB ����,$??$ HE=OE-OH = 2\ \mathrm {cm}$?
即?$GF $?到?$AB$?的距離為?$2\ \mathrm {cm},$?
∴點?$G ���、$??$ F $?也是圓上到?$AB$?距離為?$2\ \mathrm {cm} $?的點
∴圓?$O$?上到直線?$l$?的距離為?$2$?的點有?$3$?個�。