解:(1)$a = 8\div50 = 0.16,$$b = 12\div50 = 0.24�,$
$c = 50×0.2 = 10,$$d = 50×0.04 = 2����。$
補(bǔ)全頻數(shù)分布直方圖。
(2)$37800×(0.2 + 0.06 + 0.04)=11340$(名)��。
答:估計(jì)日行走步數(shù)超過(guò)12000(包含12000)的教師有11340名����。
(3)設(shè)步數(shù)$x$滿足$16000\leq x<20000$的3名教師分別為A��、B����、C�,
步數(shù)$x$滿足$20000\leq x<24000$的2名教師分別為X、Y�,
畫(huà)樹(shù)狀圖如下:
?
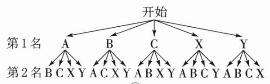
由樹(shù)狀圖可知,隨機(jī)選取日行走步數(shù)超過(guò)?$16000($?包含?$16000)$?
的?$2$?名教師共有?$20$?種等可能的結(jié)果�,其中被選取的?$2$?名教師日
行走步數(shù)恰好都在?$20000$?以上?$($?包含?$20000)$?的有?$(X,$??$Y)���、$??$(Y����,$??$X)$?這?$2$?種結(jié)果�����,
所以被選取的2名教師日行走步數(shù)恰好都在20000以上(包含
20000)的概率為$\frac{2}{20}=\frac{1}{10}��。$