解:?$(2)$?設(shè)?$∠BAG = x�。$?
∵?$AE\perp AB����,$?
∴?$∠EAG = 90°-∠BAG = 90°-x。$?
∵?$AG $?平分?$∠EAM�����,$?
∴?$∠EAM = 2∠EAG = 180°-2x�,$?
∴?$∠BAM = 90°-∠EAM = 2x - 90°。$?
∵?$MN// PQ����,$??$AB// CD,$?
∴?$∠ABQ=∠BAM�,$??$∠CDQ=∠ABQ,$?
∴?$∠CDQ=∠BAM = 2x - 90°�。$?
∵?$CD\perp DF,$?
∴?$∠FDQ = 90°+∠CDQ = 2x�����,$?
∴?$2∠BAG=∠FDQ。$?
?$ (3)∠HBD+∠AHB+∠BAH = 240°$?或
?$∠AHB+∠BAH-∠HBD = 120°�。$?
理由如下:
如圖①,當(dāng)點?$H$?在點?$K$?上方時���,過點?$H$?
作?$HT// MN�����,$?則?$HT// MN// PQ��,$?
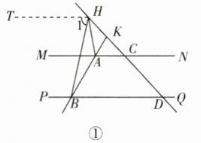
∴?$∠1=∠HBD�����,$??$∠MAB=∠ABD = 60°�����,$?
?$∠AHT+∠HAM = 180°����,$?
∴?$∠HBD+∠AHB+∠HAM = 180°��,$?
∴?$∠HBD+∠AHB+∠HAM+∠MAB = 240°,$?
即?$∠HBD+∠AHB+∠BAH = 240°�����;$?
如圖②�����,當(dāng)點?$H$?在點?$C��,$??$K$?之間時���,過點?$H$?作
?$HT// MN,$?則?$HT// MN// PQ��,$?
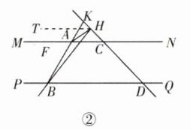
∴?$∠HBD=∠THB����,$??$∠THA=∠HAC,$?
?$∠BAC = 180°-∠ABD = 120°��,$?
∴?$∠HBD=∠THA+∠AHB=∠AHB+∠HAC$?
∴?$∠HBD=∠AHB+∠BAH-∠BAC���,$?
∴?$∠AHB+∠BAH-∠HBD=∠BAC��,$?
即?$∠AHB+∠BAH-∠HBD = 120°���;$?
如圖③����,當(dāng)點?$H$?在點?$C����,$??$D$?之間時,過點?$H$?作
?$HT// MN�����,$?則?$HT// MN// PQ����,$?
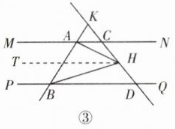
∴?$∠HAN=∠AHT,$??$∠BHT=∠HBD����,$?
?$∠BAC = 180°-∠ABD = 120°,$?
∴?$∠AHT = 120°-∠BAH���,$?
∴?$∠AHB=∠AHT+∠BHT $?
?$= 120°-∠BAH+∠HBD���,$?
∴?$∠AHB+∠BAH-∠HBD = 120°����。$?
當(dāng)點?$H$?在點?$K$?或點?$C$?處時����,經(jīng)檢驗,符合
?$∠AHB+∠BAH-∠HBD = 120°�。$?
綜上所述��,滿足條件的關(guān)系是
?$∠HBD+∠AHB+∠BAH = 240°$?或
?$∠AHB+∠BAH-∠HBD = 120°�。$?